1.前言
前面提到的算法都是通过一个函数来拟合数据解决问题,也就是单个机器学习算法,与其相对的还有多个机器学习算法,即:集成方法。
集成方法来源:如果模型之间近似相互独立,则多个模型联合的性能要优于单个模型。大致上可以分成两类:(一)把几种不同的机器学习算法集合到一起(二)把一种算法的不同参数组合起来。
集成方法由两层算法组成。底层的算法叫基学习器或者弱学习器,是单个机器学习算法,然后这些算法被集成到高层的一个方法中。
梯度提升算法(Gradient Boosting)属于把一种算法的不同参数组合起来的方式。
2.关于梯度提升算法
梯度提升算法是由Bagging算法改进而来。
Bagging算法的基本原理:从数据集中有放回的随机取样,每次抽取一定比例的数据作为训练样本,剩下的数据作为测试样本。重复以上动作n次,然后对每次动作训练一个基学习器,然后把这些学习器组合到一起,成为集合算法。由于n的不确定性,所以并不是所有的基学习器都会参与到最后的集合算法中去,后面会介绍如何进行筛选。
梯度提升算法的改进:训练基学习器的训练数据不再关注抽样的数据,而是关注由前一次训练之后产生的数据偏差。也就是说下一个模型接收的训练数据是上一个模型训练之后与目标值做对比之后产生的偏差数据。
3.数学公式
1)形式一:
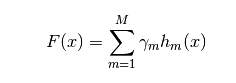
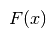 表示最后的函数,hm(x)是基学习器函数,
表示最后的函数,hm(x)是基学习器函数,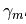 可以理解为系数。对上述公式换一下表达方式:
可以理解为系数。对上述公式换一下表达方式:
2)形式二:
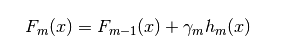
对比梯度提升法的思路,可以明白: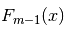 为上一个模型的输出,
为上一个模型的输出, 为当前模型。
为当前模型。
3)形式三:
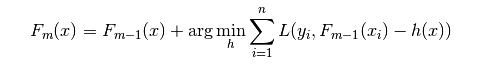
此形式,就是实现算法的基本思路,主要部分是: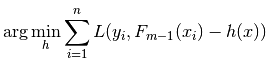 。
。
式一中的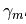 ,就是这里的
,就是这里的 函数:即求得一个最小的损失函数。
函数:即求得一个最小的损失函数。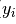 表示上一个模型训练完成的偏差值,
表示上一个模型训练完成的偏差值, 表示上一个模型,
表示上一个模型, 表示当前模型(基学习器)。
表示当前模型(基学习器)。
4.算法的基本思路
1) 初始化残差
2) 对于m=1,2,3,4....M
(a)计算残差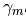 =
=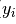 -
- ,m=1,2,3,4....M
,m=1,2,3,4....M
(b)拟合残差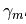 ,得到一个新的回归树Fm(x)
,得到一个新的回归树Fm(x)
(c)更新残差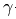 m+1=
m+1=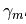 -Fm(x)
-Fm(x)
3)得到回归梯度提升树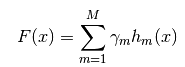
5.实现代码
1)构造合成数据。构造1000个-0.5~+0.5的等分数据用于测试,并构造对应的目标值。目标值是在测试数据上加一些小范围的随机值
import numpy import matplotlib.pyplot as plot from sklearn import tree from sklearn.tree import DecisionTreeRegressor import random ''' 第一步:构造合成数据 ''' #建立一个1000数据的测试集 nPoints = 1000 #x的取值范围:-0.5~+0.5的nPoints等分 xPlot = [-0.5+1/nPoints*i for i in range(nPoints + 1)] #y值:在x的取值上加一定的随机值或者叫噪音数据 #设置随机数算法生成数据时的开始值,保证随机生成的数值一致 numpy.random.seed(1) ##随机生成宽度为0.1的标准正态分布的数值 ##上面的设置是为了保证numpy.random这步生成的数据一致 y = [s + numpy.random.normal(scale=0.1) for s in xPlot]
2)生成测试需要的训练集和测试集
''' 第二步:构造训练集和测试集-->随机抽取30%作为测试集,其余70%作为训练集 ''' ##测试集大小 nSample = int(nPoints * 0.30) ##在0~npoints直接随机生成nSample个点 idxTest = random.sample(range(nPoints), nSample) #定义训练集和测试集标签 xTrain = [] #训练集 xTest = [] #测试集 yTrain = [] #训练集标签 yTest = [] #测试集标签 ##划分数据 for i in range(nPoints): if i not in idxTest: xTrain.append(xPlot[i]) yTrain.append(y[i]) else : xTest.append(xPlot[i]) yTest.append(y[i])
3)构建模型列表,即:集合方法。这里重点说下步长,即参数eps:调整其值,使均方误差最小值在或者接近图右侧,以达到最佳性能(下图2)
''' 第三步:构建模型列表,即:集合方法 核心思路: 1)初始化残差列表 2)在循环中 a)计算残差 b)使用残差拟合新回归树 c)更新残差 3)获得模型列表 ''' ##初始化产生的最大二元决策树的数量 numTreesMax = 30 ##树的深度---这个是需要不断调整的 treeDepth = 5 ##模型列表:二元决策树列表 modelList = [] ##预测值列表 predList = [] ##步长,使函数可以更快的收敛:调整eps值,使均方误差最小值在或者接近图右侧 eps = 0.1 #初始化残差函数:由于初始化时预测值为空,所以是实际值 residuals = list(yTrain) ##开始生成模型列表 for iTrees in range(numTreesMax): ##添加新二元决策树到模型列表 modelList.append(DecisionTreeRegressor(max_depth=treeDepth)) ##通过最新的二元决策树拟合数据 modelList[-1].fit(numpy.array(xTrain).reshape(-1, 1), residuals) ##使用最新的模型预测数据 latestInSamplePrediction = modelList[-1].predict(numpy.array(xTrain).reshape(-1, 1)) ##更新残差 residuals = [residuals[i] - eps * latestInSamplePrediction[i] for i in range(len(residuals))] ##在测试集上使用模型 latestOutSamplePrediction = modelList[-1].predict(numpy.array(xTest).reshape(-1, 1)) ##加入预测值列表 predList.append(list(latestOutSamplePrediction))
4)筛选合适的列表长度,即筛选进入集合的模型
筛选方法:不断累加模型在测试集上的误差值,直到这个和值基本保持不变了(即图像尾部区域直线),此时的模型个数是最优的模型个数。为了方便理解下面循环,用个图解释下:
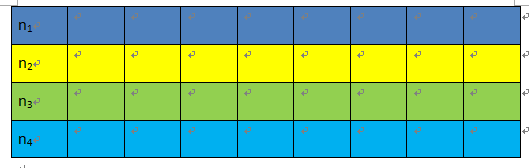
(图1)
测试集经过在所有的模型上计算后,会形象一个二维的列表(如上图1所示)。每一行代表一个模型的预测结果。第一次循环就是n1的数据,第二次循环是n1+n2的值,第三次循环存储的是n1+n2+n3的值,依次类推,直到把模型列表循环完成。
##均方差列表 mse = [] ##在测试集上的预测值之和的列表 allPredictions = [] i=0 ##通过误差累计的方式筛选列表 for iModels in range(len(modelList)): prediction = [] ##此循环的目的:每个模型都是把前面的所有的模型的预测值加起来,形成一个新列表 for iPred in range(len(xTest)): prediction.append(sum([predList[i][iPred] for i in range(iModels + 1)]) * eps) ##添加到列表 allPredictions.append(prediction) ##计算新的离差 errors = [(yTest[i] - prediction[i]) for i in range(len(yTest))] ##均方差:即离差的平方和的平均数 mse.append(sum([e * e for e in errors]) / len(yTest))
5)绘图观察结果
''' 第五步:绘图观察结果 ''' ##模型个个数+1,绘图用:即模型列表中的从0开始的下标变成从1开始 的编号 nModels = [i + 1 for i in range(len(modelList))] ##绘制均方差和模型个数变化曲线 plot.plot(nModels,mse) plot.axis('tight') plot.xlabel('Number of Models in Ensemble') plot.ylabel('Mean Squared Error') plot.ylim((0.0, max(mse))) plot.show() ##绘制模型曲线和真实值曲线的对比 plotList = [0, 14, 29] lineType = [':', '-.', '--'] plot.figure() for i in range(len(plotList)): iPlot = plotList[i] textLegend = 'Prediction with ' + str(iPlot) + ' Trees' plot.plot(xTest, allPredictions[iPlot], label = textLegend, linestyle = lineType[i]) plot.plot(xTest, yTest, label='True y Value', alpha=0.25) plot.legend(bbox_to_anchor=(1,0.3)) plot.axis('tight') plot.xlabel('x value') plot.ylabel('Predictions') plot.show()


(图2) (图三)
6.使用sklearn包中的函数实现上述功能
1)主要函数几参数介绍
a)mean_squared_error 均方误差函数
b)ensemble.GradientBoostingRegressor 梯度上升法函数
主要参数:
n_estimators:回归树的个数
max_depth:回归树的深度
learning_rate:学习率,即步长
subsample:默认为1,算法发明人建议设置成1
loss:选择损失函数
2)实现过程(略去了数据生成部分,代码同上)
import numpy import matplotlib.pyplot as plot from sklearn import tree from sklearn import ensemble from sklearn.metrics import mean_squared_error import random ''' 第三步:调用函数处理数据 loss:“ls” 表示内部使用最小均方误差算法 ''' ##树的个数 nEst = 30 ##树的深度 depth = 5 ##学习率,即步长 learnRate = 0.1 ##建议值0.5 subSamp = 0.5 ##定义函数 GBMModel = ensemble.GradientBoostingRegressor(n_estimators=nEst, max_depth=depth, learning_rate=learnRate, subsample = subSamp, loss='ls') ##在训练集上训练数据 GBMModel.fit(numpy.array(xTrain).reshape(-1, 1), yTrain) ##均方误差列表 msError = [] ##计算模型在测试集上的预测值 predictions =GBMModel.staged_predict(numpy.array(xTest).reshape(-1, 1)) ##计算测试集上预测值的均方误差 for p in predictions: msError.append(mean_squared_error(numpy.array(yTest).reshape(-1, 1), p)) #print("MSE" ) #print(min(msError)) #print(msError.index(min(msError))) ''' 第四步:绘图 ''' plot.figure() plot.plot(range(1, nEst + 1), GBMModel.train_score_, label='Training Set MSE') plot.plot(range(1, nEst + 1), msError, label='Test Set MSE') plot.legend(loc='upper right') plot.xlabel('Number of Trees in Ensemble') plot.ylabel('Mean Squared Error') plot.show()
结果如图:

可以看到,测试集曲线(绿色)的趋势和上面图2的趋势基本一致:误差在0.0103左右,曲线区域平稳后的树的数目在25左右