以下摘自Proverbs的博客:
1. 首先进行构图,对于那么对流量没有限制的边,我们直接将容量赋值为原始的容量,而对于有流量要求的边,我们将容量减去下界并将其等价与无下界的边。
2. 添加一个附加汇点和一个附加源点,从附加源点连向每个顶点的容量为以该点所有流入的下界流量总和,每个顶点流向附加汇点是该点流出的下界流量总和。
3. 添加一条从汇点到源点流量为INF的边,这条边的意义在于,能够使得源点会汇点满足成为流量平衡条件的普通节点。
4. 我们在以附加源点和附加汇点求一次最大流,如果所有的到附加汇点的边都满载,那么说明这个网络是存在满足所有下界的可行流的。

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using std::min; 5 using std::max; 6 #define M 100000 7 #define N 1000 8 #define INF 210000000 9 #define rep(i,n) for(int i=1;i<=(n);i++) 10 #define mem(a) memset(a,0,sizeof(a)) 11 int len[M <<1],e[M <<1],nex[M <<1],other[M <<1],head[N],last[N],d[N],num[N]; 12 int rdu[N],cdu[N],_,eee,flag,y,k,l,opt,S,T,m,n,ans,tot,ss,tt,ee,x,uu[250][250],dd[250][250]; 13 int an[250][250]; 14 char c; 15 struct lbz 16 { 17 int u,v,l,r; 18 }a[N]; 19 void init() 20 { 21 memset(head,0,sizeof(head)); 22 memset(num,0,sizeof(num)); 23 memset(d,0,sizeof(d)); 24 mem(cdu); 25 mem(rdu); 26 rep(i,n) 27 rep(j,m) 28 { 29 uu[i][j]=INF; 30 dd[i][j]=0; 31 } 32 flag=ans=ee=eee=0; 33 } 34 void add(int u,int v,int c) 35 { 36 //printf("%d %d %d ",u,v,c); 37 other[++ee]=ee+1; 38 e[ee]=v;nex[ee]=head[u];head[u]=ee;len[ee]=c; 39 other[++ee]=ee-1; 40 e[ee]=u;nex[ee]=head[v];head[v]=ee;len[ee]=0; 41 } 42 int dfs(int x,int flow) 43 { 44 int rec,j,p; 45 if (x==tt) return flow; 46 rec=0;j=last[x]; 47 while (j!=0) 48 { 49 if (len[j]>0 && d[x]==d[e[j]]+1) 50 { 51 last[x]=j; 52 p=dfs(e[j],min(len[j],flow-rec)); 53 len[j]-=p;len[other[j]]+=p; 54 rec+=p; 55 if (rec==flow) return rec; 56 } 57 j=nex[j]; 58 } 59 if (d[ss]>tot) return rec; 60 if (--num[d[x]]==0) d[ss]=tot; 61 last[x]=head[x]; 62 num[++d[x]]++; 63 return rec; 64 } 65 void deal(int x,int y) 66 { 67 if (c=='>') 68 dd[x][y]=max(dd[x][y],k+1); 69 if (c=='<') 70 uu[x][y]=min(uu[x][y],k-1); 71 if (c=='=') 72 { 73 if (k<dd[x][y]||k>uu[x][y]) 74 flag=1; 75 dd[x][y]=uu[x][y]=k; 76 } 77 if (uu[x][y]<dd[x][y]) 78 flag=1; 79 } 80 void add1(int u,int v,int l,int r) 81 { 82 eee++; 83 a[eee].u=u;a[eee].v=v; 84 a[eee].l=l;a[eee].r=r; 85 rdu[v]+=l;cdu[u]+=l; 86 } 87 int main() 88 { 89 scanf("%d",&_); 90 int __=_; 91 while (_--) 92 { 93 if (__!=_-1) puts(""); 94 scanf("%d%d",&n,&m); 95 init(); 96 S=2;T=n+m+3; 97 rep(i,n) 98 { 99 scanf("%d",&l); 100 add1(S,i+2,l,l); 101 } 102 rep(i,m) 103 { 104 scanf("%d",&l); 105 add1(n+i+2,T,l,l); 106 } 107 scanf("%d",&opt); 108 while (opt--) 109 { 110 scanf("%d%d %c %d",&x,&y,&c,&k); 111 if (x==0&&y==0) 112 { 113 rep(i,n) 114 rep(j,m) 115 deal(i,j); 116 continue; 117 } 118 if (x==0) 119 { 120 rep(i,n) 121 deal(i,y); 122 continue; 123 } 124 if (y==0) 125 { 126 rep(i,m) 127 deal(x,i); 128 continue; 129 } 130 deal(x,y); 131 } 132 if (flag==1) 133 { 134 printf("IMPOSSIBLE "); 135 continue; 136 } 137 rep(i,n) 138 rep(j,m) 139 { 140 add1(i+2,j+2+n,dd[i][j],uu[i][j]); 141 } 142 ss=S-1;tt=T+1; 143 rep(i,eee) 144 add(a[i].u,a[i].v,a[i].r-a[i].l); 145 for (int i=S;i<=T;i++) 146 { 147 add(ss,i,rdu[i]); 148 add(i,tt,cdu[i]); 149 } 150 add(T,S,INF); 151 152 tot=num[0]=tt; 153 for (int i=ss;i<=tt;i++) 154 last[i]=head[i]; 155 while (d[ss]<tot) 156 ans+=dfs(ss,2147483647); 157 //printf("%d ",ans); 158 int j=head[ss]; 159 while (j>0) 160 { 161 if (len[j]>0) 162 flag=1; 163 j=nex[j]; 164 } 165 if (flag==1) 166 { 167 printf("IMPOSSIBLE "); 168 continue; 169 } 170 for (int i=3;i<=2+n;i++) 171 { 172 int j=head[i]; 173 while (j>0) 174 { 175 an[i-2][e[j]-n-2]=dd[i-2][e[j]-n-2]+len[other[j]]; 176 j=nex[j]; 177 } 178 } 179 rep(i,n) 180 { 181 rep(j,m-1) 182 printf("%d ",an[i][j]); 183 printf("%d ",an[i][m]); 184 } 185 186 } 187 return 0; 188 }
以下摘自Edelweiss《网络流建模汇总》
发散思维:
1. 怎样求无源汇有上下界网络的可行流?
由于有源汇的网络我们先要转化成无源汇,所以本来就无源汇的网络不用再作特殊处理。
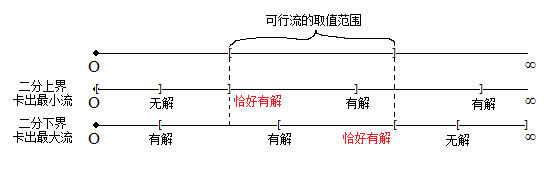
2. 怎样求无源汇有上下界网络的最大流、最小流?
一种简易的方法是采用二分的思想,不断通过可行流的存在与否对(t, s)边的上下界U, L进行调整。求最大流时令U = ∞并二分L;求最小流时令L = 0并二分U。道理很简单,因为可行流的取值范围是一段连续的区间,我们只要通过二分找到有解和无解的分界线即可。