若 (AB=4,overrightarrow{AC}=3overrightarrow{CB}) ,平面内一点 (P) ,满足 (dfrac{overrightarrow{PA}cdotoverrightarrow{PC}}{|overrightarrow{PA}|}=dfrac{overrightarrow{PB}cdotoverrightarrow{PC}}{|overrightarrow{PB}|}) ,(sinangle PAB) 的最大值是 (underline{qquadqquad}) .
【解析】
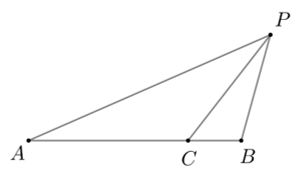
如图,依题意有
[dfrac{|overrightarrow{PA}||overrightarrow{PC}|cosangle APC}{|overrightarrow{PA}|}=dfrac{|overrightarrow{PB}||overrightarrow{PC}|cosangle BPC}{|overrightarrow{PB}|}Longrightarrow angle APC=angle BPC
]
因为 (overrightarrow{AC}=3overrightarrow{CB}) ,所以 (|AC|=3|CB|) ,根据角平分线定理得
[dfrac{|AP|}{|BP|}=dfrac{|AC|}{|CB|}=3
]
设 (|BP|=a) ,则 (|AP|=3a) ,则
[cosangle PAB=dfrac{9a^2+16-a^2}{2cdot3acdot4}=dfrac{a}{3}+dfrac{2}{3a}geqslant2sqrt{dfrac{a}{3}cdotdfrac{2}{3a}}=dfrac{2sqrt2}{3}
]
当且仅当 (dfrac{a}3=dfrac{2}{3a}) ,即 (a=sqrt2) 时,(cosangle PAB) 最小值为 (dfrac{2sqrt2}{3}) ,易知 (angle PABinBig(0,dfrac{pi}{2}Big)) ,故此时 (sin angle PAB) 取最大值 (dfrac13) .