p1268树的重量 题解

题面描述点此qwq。

正解开始。

一道茅塞顿开恍然大悟的题目：

第一眼看到这个题的时候，语文不好的我对着题目中的

这些，和：

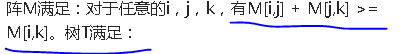
这句话发呆半天，，，，

因为不关我怎么构建几何模型，我都不理解这句话。。

（吐槽题面臃肿！）

 然后想了一下，发现题目是这个亚子：

给你一个矩阵M，M上每一个节点（i，j）表示叶子结点i和叶子结点j的距离，每个矩阵有且只能生成唯一一个树（不然这题没法搞了），让你求这棵树上的每一条边的权值和。

在李姐（lz dalao）完题目之后，我又开始懵了。。。。。。到底怎么搞非叶节点的位置？？？暴力恐怕不行的。。

百思不得其解后，我在绝望中从最简单情况递推：

考虑只有两个（n=2）节点1，2，一条边权值为3

这种情况：

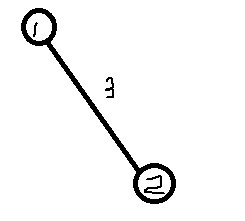
那么，两个节点自然权值就为3了，答案也是3。

一旦跨越到n=3这种情况，就有些棘手。

因为3个节点都是叶子结点，那么必然要在1到2的路径上选一个中间节点来连接3号节点。

（选哪里好呢..?）

因为1到3和2到3的长度都知道了，那么我们可以利用数学方法求助3的位置。

假设M[1][3]=4,M[2][3]=3，那么这两条路径必然有和1到2的路径重复的。

那么我们减去重复的，就是3节点到1，2路径的距离了。

如图：

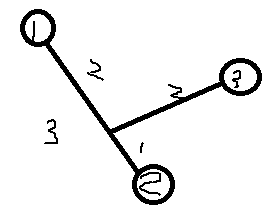
公式：(jz[1][3]+jz[2][3]-jz[1][2])/2=(4+3-3)/2=2.

那么，理解了这个以后，我们可以顺着推n>3的情况：

从之前n-1的情况中找两个点之间的路径，并尝试插入当前节点，然后取min。

节点太多就不画了。。

上代码吧。。

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

inline int read()
{
    int ans=0;
    char ch=getchar(),last=' ';
    while(ch<'0'||ch>'9')last=ch,ch=getchar();
    while(ch>='0'&&ch<='9')ans=(ans<<3)+(ans<<1)+ch-'0',ch=getchar();
    return last=='-'?-ans:ans;
}

int n,jz[100][100];

int main(){
    n=read();
    while(n!=0)
    {
        for(int i=1;i<=n;i++)
            for(int j=i+1;j<=n;j++)
                jz[j][i]=read(),jz[i][j]=jz[j][i];
        int ans=jz[1][2];
        for(int i=3;i<=n;i++)
        {
            int dt=0x3f3f3f3f;
            for(int j=1;j<=i-1;++j)
                for(int k=1;k<=j-1;++k)
                {
                    dt=min(dt,(jz[j][i]+jz[k][i]-jz[j][k])>>1);
                }
        ans+=dt;
        }
        printf("%d
",ans);
        n=read();
    }
}

完结。