差分约束详解&&洛谷SCOI2011糖果题解

差分约束系统：

如果一个系统由n个变量和m个约束条件组成，形成m个形如ai-aj≤k的不等式(i,j∈[1,n],k为常数),则称其为差分约束系统(system of difference constraints)。亦即，差分约束系统是求解关于一组变量的特殊不等式组的方法。

　　　　——度娘。

然而并没有看懂。。

通俗来说，满足差分约束的条件是题目中给了你多个ai-aj<=(>=,<,>之类)的条件，要求同时满足这些条件并求极值的问题。

内么，怎么同时满足这些问题呢？

假如我们以这个东西为例:

a2<a1,a2<a3,a3<a1。并要求同时满足求满足条件的a的和的最小值。（a>=0）

那么，我们可以用图来描述这个问题：

我们设有向边（u，v），边权为1表示u>v。因为u>v等价于u-1>=v,也就是u-v>=1，那么我们就将（u，v），权值i理解为u-v=i。

画出来图长这样：

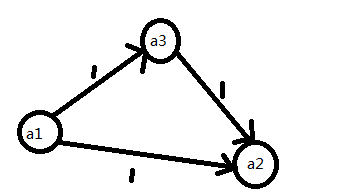
要满足所有条件且最小，也就是满足a1-a2=1，a1-a3+（a3-a2）=2。

整理得：a1-a2=1；a1-a2=2；

取最大的那个。

在图上表示，就（莫名其妙的）变成了求最长路！

很神奇吧qwq。

也就是说，如果你想满足所有条件，就先建图，然后根据题目情况（最短路求得未知数最大，最长路求得未知数最小）来跑最长/短路。

例题：SCOI2011糖果：

跑最长路qwq：

code：

#include<cstdio>
#include<cstring>
#include<queue>
#include<iostream>
#include<cstdlib>
using namespace std;

int n,k,x,a,b,sum=0,head[200002],cnt[200002],dis[200002];
long long ans=0;
queue<int> q;
bool vis[200002];

inline int read()
{
    int ans=0;
    char ch=getchar(),last=' ';
    while(ch>'9'||ch<'0')last=ch,ch=getchar();
    while(ch>='0'&&ch<='9')ans=(ans<<3)+(ans<<1)+ch-'0',ch=getchar();
    return last=='-'?-ans:ans;
}

struct edge{
    int next,to,dis;
}edg[210001];

inline void add(int from,int to,int dis)
{
    edg[++sum].dis=dis;
    edg[sum].to=to;
    edg[sum].next=head[from];
    head[from]=sum;
}

int main(){
    n=read();k=read();
    for(int i=1;i<=k;i++)
    {
        x=read(),a=read(),b=read();
        if(x==1){
            add(a,b,0);add(b,a,0);
        }
        if(x==2){
            if(a==b){
                printf("-1");return 0;
            }
            add(a,b,1);
        }
        if(x==3){
            add(b,a,0);
        }
        if(x==4){
            if(a==b){cout<<-1;return 0;}
            add(b,a,1);
        }
        if(x==5){
            add(a,b,0);
        }
    }
    for(int i=1;i<=n;i++)add(0,i,1);
    vis[0]=1;q.push(0);
    while(!q.empty()){
        int now=q.front();q.pop();vis[now]=0;
        if(cnt[now]==n-1){
            printf("-1");return 0;
        }
        cnt[now]++;
        for(int i=head[now];i;i=edg[i].next)
        {
            int v=edg[i].to;
            if(dis[v]<dis[now]+edg[i].dis){
                dis[v]=dis[now]+edg[i].dis;
                if(!vis[v])vis[v]=1;q.push(v);
            }
        }
    }
    for(int i=1;i<=n;i++)
    {
        ans+=dis[i];
    }
    printf("%lld
",ans);
}

完结qwq