依然zhx讲。
讲了概率与期望:
期望:事件结果的平均大小。记作E(x)。
E(x)=每种结果的大小与其概率的乘积的和。
例如,记掷一枚骰子的点数为x
E(x)=1*(1/6)+2*(1/6)+3*(1/6)+4*(1/6)+5*(1/6)+6*(1/6)=7/2
若c为常数,那么:
E(x+c)=E(x)+c,E(c*x)=c*E(x)。
如果记两个事件的结果分别为x,y,那么他们自然满足以下性质:




E(x+y)=E(x)+E(y)
例如:E(语文成绩+数学成绩)=E(语文成绩)+E(数学成绩)
若两个事件互相独立,E(x*y)=E(x)*E(y)
E(语文成绩*数学成绩)=E(语文成绩)*E(数学成绩)
其中,第一个性质在任何情况下满足,第二个一定要满足事件独立!
概率和期望的计算
概率与期望的计算有一个共同的计算技巧:
若事件所产生的所有方案都是等概率的,那么一些概率与期望即可转化
为一个计数问题,算出后再除以总方案数即可。
如求事件符合条件A的概率,则转化为对符合A的方案数的计数问题;若
求方案的某种价值的期望值,则转化为所有方案的价值总和的计数问题。
emmmmm。。。举个栗子qwq
概率与期望还可以通过列方程的方法计算。
有4张卡片,写着0,1,2,3,每次抽出一张并放回,反复抽,抽出0为止。问
抽取的次数的期望值。
设抽取次数为x,则:x=1+x*3/4
x=4。
上题:






对于每一个边,走过的概率为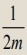
那么每个点的概率即为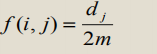
于是答案就是: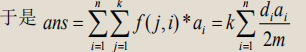






斜率优化:

万能套用代码: 。d+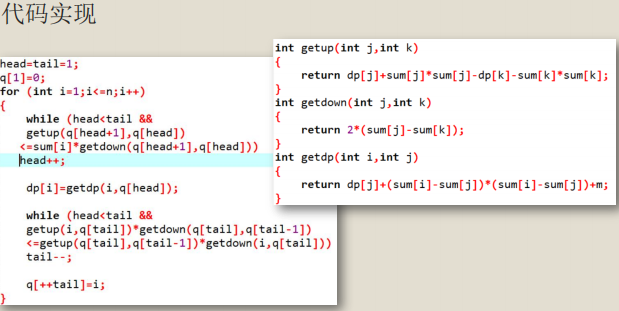
欢送赵和旭qwq。上午结束辣。
下午,恭迎杨思祺 。
。
一个把poj(p欧接)念成poj(p欧勾)的神仙。
图论:
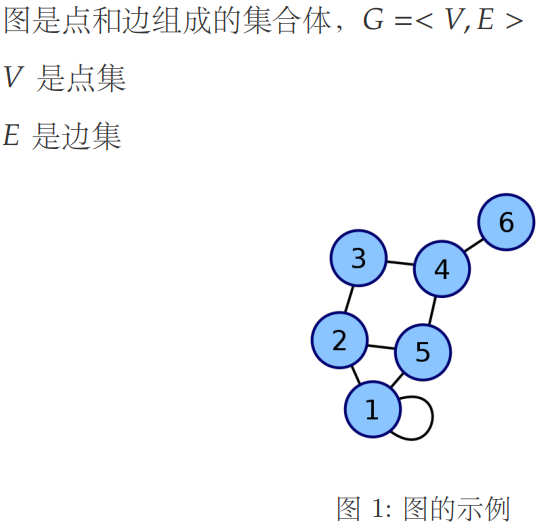
边: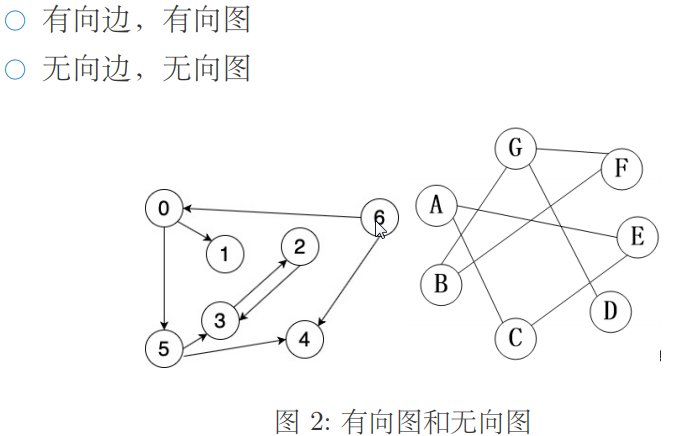
老师准备的很认真,开始知识很基础(shui)。

点权:赋给点的数值。
边权:赋给边的数值。
负权:边的权值为负。

有向无环图:dag(大哥)。

树:不用解释。。
完全图:任意两个点间都有一条直接相连的边。
竞赛图:有向边(版本)坂本的完全图
基环树:在树(n个节点,n-1条边)的基础上,任意加一条边(n个节点,n个边),有且仅有一个简单环。
仙人掌:存在环,但是任意一个边不属于两个环的图
邻接矩阵存图:

链式前向星(邻接表存图)

图的遍历:


二叉树遍历:



思路:构建最短路图并统计入度,如果入度大于1,就不影响。等于一,一定会影响。

裸拓扑排序。跑的时候判个环就行


上最短路:

分为全局(floyd)最短路,单源(dij,spfa)最短路。
dij:
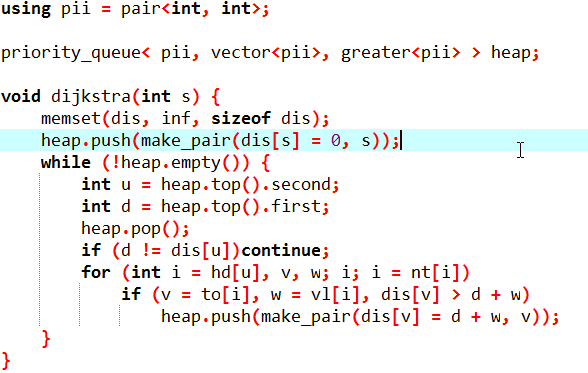
spfa:

今天就这样了,后半天还挺水的。。。。。
完结。