今天讲图论
图是啥?(白纸上的符号?)
对于一个拥有n个顶点的无向连通图,它的边数一定多于n-1条。若从中选择n-1条边,使得无向图仍然连通,则由n个顶点及这 n-1条边(弧)组成的图被称为原无向图的生成树。
换句话说,有边有点就是图。(本蒟蒻的理解是这样。。QWQ)
另外,还有一些与图有关的定义(很好理解,通俗一点):
阶:图中点的个数。
边:两个点间的连接
权值:边的长度
。。。想了解更多找度娘,她可能讲的比我通俗QWQ。
邻接矩阵:
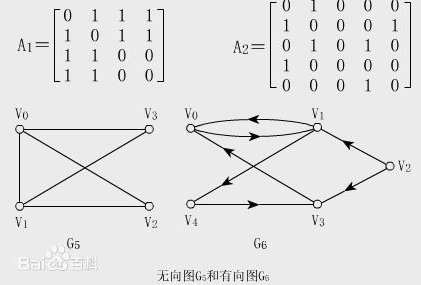

存图方式:邻接矩阵,链式前向星
1.邻接矩阵:用两个角标存储,f[i][j]表示从i到j的边的权值
2.链式前向星:
void addedge(long long from,long long to,long long dis)//入边链式前向星 { num_edge++;//编号 edge[num_edge].next=head[from];//把next值改为此边编号 edge[num_edge].to=to;//to和dis分别为对应的终点和长度 edge[num_edge].dis=dis; head[from]=num_edge;//把这个边的始点的编号的head值改为前一个边的编号(指向) }
最小生成树:从图中选出一些边和结点,使得每个结点都被联通,且保证边权之和最小
克鲁斯卡尔:

最短路径算法:
floyd:

代码为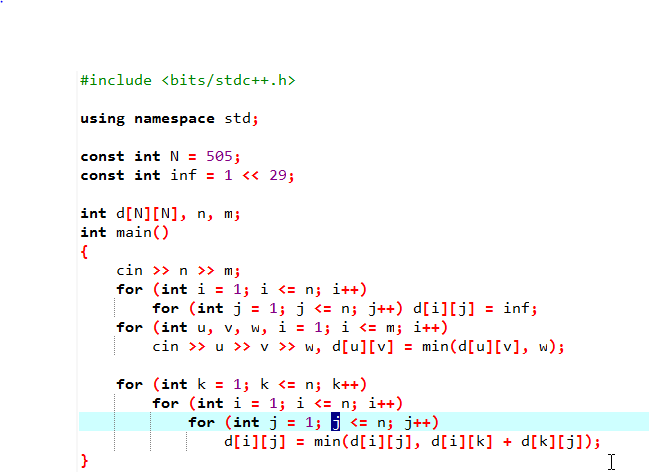 三重循环
三重循环
比尔曼福德:
Bellman - ford算法是求含负权图的单源最短路径的一种算法,效率较低,代码难度较小。其原理为连续进行松弛,在每次松弛时把每条边都更新一下,若在n-1次松弛后还能更新,则说明图中有负环,因此无法得出结果,否则就完成。

DAG(大哥):
