今天讲基础数据结构
首先讲(二叉搜索树)


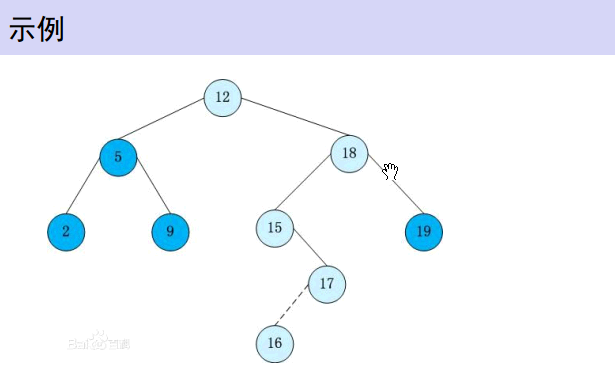



保证左儿子小于右儿子,那么对于根节点来说。大于根节点的放到右子树递归,小于根节点的放在左子树
相等的呢?某大佬(老师)这么说:



删除的前提是找这个点在哪:



如果两个儿子咋办。

再回忆一遍;左儿子的值小于父亲节点的值
右儿子的值大于父亲节点的值
搞一个高度为logn的搜索树:


对于二叉搜索树,它可以通过中序排列大小:


然后是堆。
堆是?https://www.cnblogs.com/lbssxz/p/10776682.html
在堆中插入一个元素,将其与父亲节点进行大小比较,直到满足条件为止(小根堆,大根堆)
删除:先将要删除的节点与堆尾(n)的节点换一下,然后将长度-1,(就是删除了),那么,交换后的n节点一定不满足堆的性质,那么只要再维护一下就行了
queue:一个队列的头文件



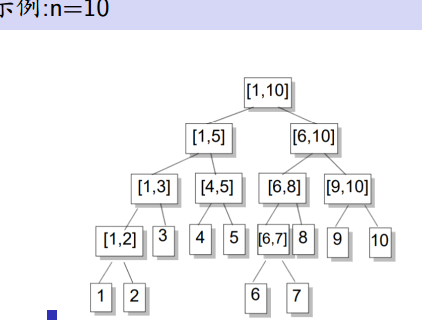
线段树:对于线段树中的每一个非叶子节点[a,b],它的左儿子表示的区间为[a,(a+b)/2],右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树,最后的子节点数目为N,即整个线段区间的长度。
简单来说就是将一个集合范围的数拆分成单个数组成的集合,每个节点不再是一个数(权值)而是一个线段长度(范围)

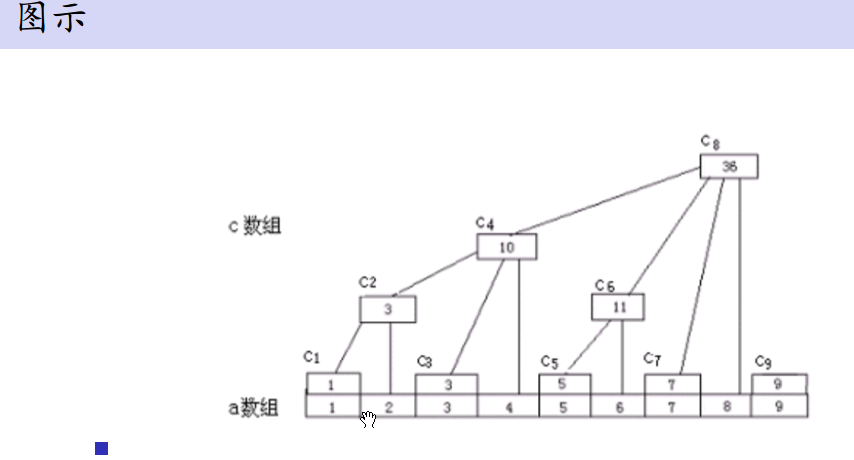
树状数组:
unique为去重,
LCA为
也就是树中两个连通结点的转折点。QAQ

(求LCA时)父亲的平方QWQ;
并查集:
将几个数组每一个自己赋一个属于自己的值,然后如果要使两个元素归为一个集合,那么把他们的值置为一个

缓口气消化一下(不良)