1.图的两种遍历方式
图的遍历通常有两种方式,即深度优先搜索(Depth First Search)和广度优先搜索(Breadth First Search)。前者类似于树的先序遍历,而后者类似于树的层次遍历。
2.深搜的实现
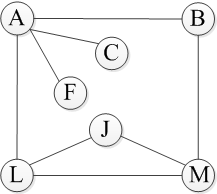
从节点A开始,找到第一个邻接点B,接着按照深搜的策略,寻找B的第一个邻接节点,结果是A,但是A已经被访问过了,所以应该选择节点M访问。同B一样,M找到邻接节点B、L和J,B被访问过,而L和J选择存储位置靠前的节点——L。接着L找到J,但是J的邻接节点全部都被访问过,因此退回节点L,同样L的所有邻接节点也全部被访问过,退回到节点M,B直到A。A访问第二个邻接点C,C没有被访问过且没有邻居节点,再退回到A,A访问F,最后一个L已被访问。
public void DFS(int i, boolean [] visited) { if (visited[i] == false) {System.out.print(vertex.get(i)); visited[i] = true;} for (int j = 0; j < visited.length; j++) { if(adj[i][j] == 1 && visited [j] == false) DFS(j,visited); } } public void DFS() { boolean [] visited = new boolean [Vnum]; for (int i = 0; i < visited.length; i++) visited[i] = false; for (int i = 0; i < visited.length; i++) if(!visited[i]) DFS(i,visited); }
测试代码
int number = 7; Graph <Character> g= new Graph<>(number); for (int j = 0; j < number; j++) g.addVertex((char)('A' + j)); g.addEdge(1,2); g.addEdge(1,3); g.addEdge(1,4); g.addEdge(1,5); g.addEdge(2,7); g.addEdge(5,6); g.addEdge(5,7); g.addEdge(7,6); g.DFS();
深度搜索结果为ABGEFCD(其中D,E,F,G代替图中的F,L,J,M)
3.广搜的实现
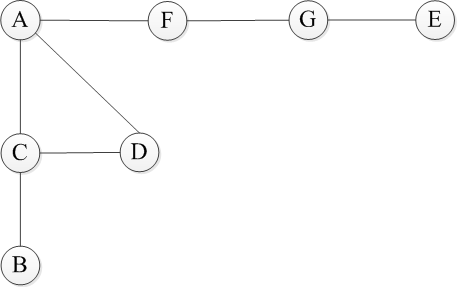
首先从A开始访问,接着按顺序访问邻接点C,D和F。然后从C开始访问邻接点B(D被访问过了),接着是D,F的邻接点。最终顺序应该是ACDFBGE。既然是借鉴树的层次遍历,可以使用如下示意图表示广度搜索。
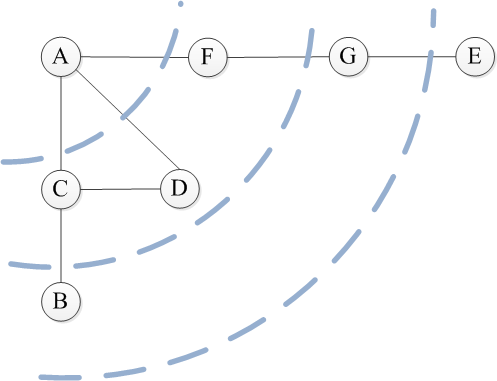
public void BFS() { boolean [] visited = new boolean [Vnum]; Queue q = new Queue(); q.AddQueue(0); for (int i = 0; i < visited.length; i++) visited[i] = false; while (!q.isEmpty()){ int m = q.OutQueue(); if (visited[m] == false) { visited[m] = true; System.out.print(vertex.get(m)); } for (int j = 0; j < visited.length; j++) { if(adj[m][j] == 1 && visited [j] == false) { q.AddQueue(j); } } } }
测试
g.addEdge(2,3); g.addEdge(1,3); g.addEdge(1,4); g.addEdge(1,6); g.addEdge(3,4); g.addEdge(5,7); g.addEdge(7,6); g.BFS();
结果ACDFBGE
全部代码查看Graph