博客园博主skywang123456(以下简称s博主)是一个大牛级的人物,相信很多程序员都拜读过他的博客,我也不例外,并且受益匪浅。但是对于文章二叉堆(三)之 Java的实现我有一些疑惑,写在这里,供有缘人参考。对于而二叉堆的插入,是一个较为简单的方法,这里没有什么问题。但是而二叉堆的删除确是一个稍微复杂一点的操作,事实上,我第一次看这篇博文的时候就感觉有些恍惚不清。一般来说,而二叉堆的删除分为删除堆顶和查找型删除。堆顶删除可以由查找型删除实现,故名思意,直接删除堆顶的数据即可,在二叉堆的实际应用中被广泛使用。而查找型删除首先要查到给定参数的位置,然后删除该元素。而我要指出的问题是博主s使用删除堆顶的代码来代替了查找型删除的代码,而这两个我会举例来说明是不同的。
先来看博主s的删除代码
public int remove(T data) { // 如果"堆"已空,则返回-1 if(mHeap.isEmpty() == true) return -1; // 获取data在数组中的索引 int index = mHeap.indexOf(data); if (index==-1) return -1; int size = mHeap.size(); mHeap.set(index, mHeap.get(size-1));// 用最后元素填补 mHeap.remove(size - 1); // 删除最后的元素 if (mHeap.size() > 1) filterdown(index, mHeap.size()-1); // 从index号位置开始自上向下调整为最小堆 return 0; }
protected void filterdown(int start, int end) { int c = start; // 当前(current)节点的位置 int l = 2*c + 1; // 左(left)孩子的位置 T tmp = mHeap.get(c); // 当前(current)节点的大小 while(l <= end) { int cmp = mHeap.get(l).compareTo(mHeap.get(l+1)); // "l"是左孩子,"l+1"是右孩子 if(l < end && cmp<0) l++; // 左右两孩子中选择较大者,即mHeap[l+1] cmp = tmp.compareTo(mHeap.get(l)); if(cmp >= 0) break; //调整结束 else { mHeap.set(c, mHeap.get(l)); c = l; l = 2*l + 1; } } mHeap.set(c, tmp); }
不难理解,将查找到的节点使用堆尾数据填充,之后删除堆尾数据,接着从该节点自上往下调整为最小堆。(目测笔误,应该是最大堆)这是典型的删除堆顶的代码。
博主s在文中给了两个删除的例子。第一个是删除堆顶的元素,因为没有根节点,所以当然适合这个代码。
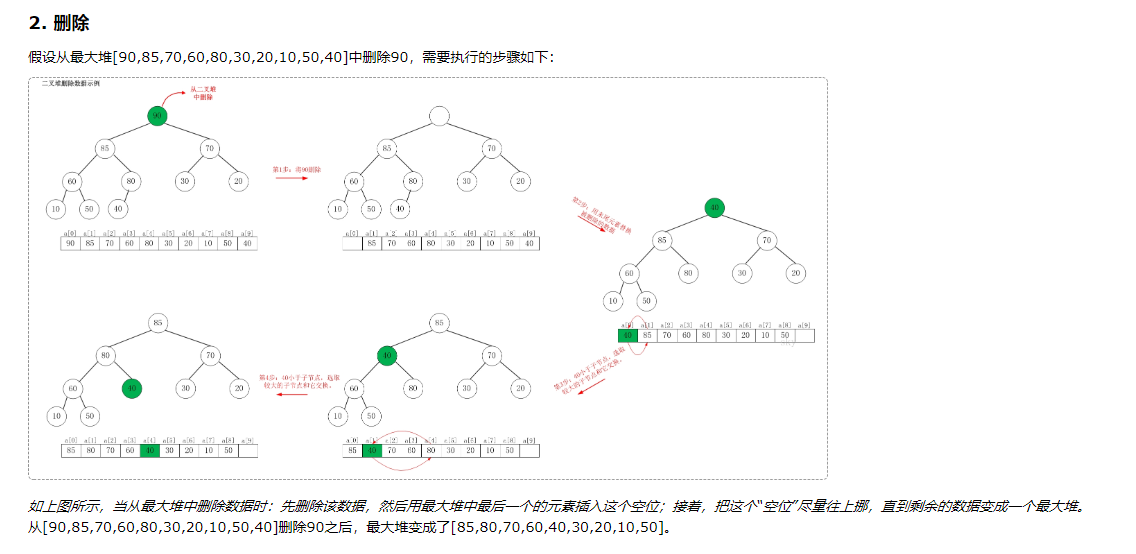
而第二个例子不是删除根节点的数据,但是为什么也可以?这是一个巧合,恰好是符合某些特定的条件。
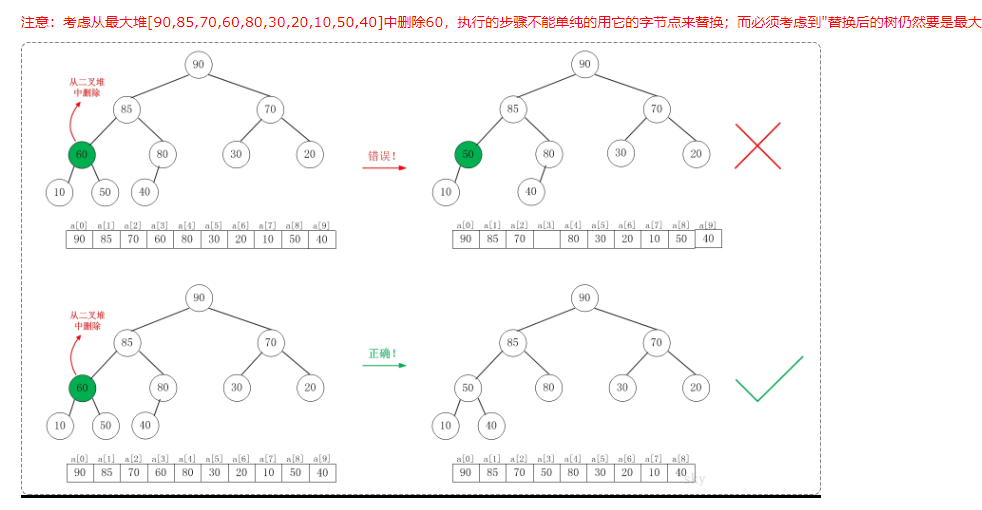
如图所示,删除节点60,补充40,40小于其子节点50,然后交换。其实有一种情况,即堆尾数据补充之后会大于原先的父节点,我们来看下图这个堆。
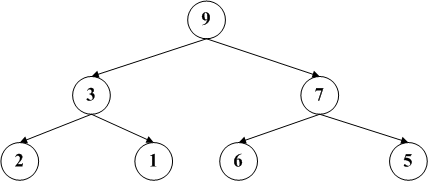
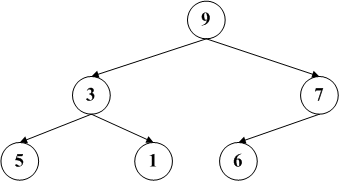
如果我们删除节点2,按照博主s的步骤,将5补充到原有节点2的位置,然后删除原有节点5,这样就变成右图。之后由于没有子节点,因此结束删除操作。可是右边是一个最大堆吗?显然不是!
所以查找型删除应该添加一个步骤,即先判断是否大于父节点(对于最大堆来说),如果大于父节点,则进行向上交换,直到符合最大堆的条件。查找型删除可以参考我这一篇文章二叉堆的介绍和Java实现 。当然我的代码没有过多测试,可能也有没有考虑到的地方,欢迎大家直接勘误。
以上,便是我看完这篇博文的一些质疑和思考,所说的不一定都对。当然,即使博主s真的有失误,也不影响我这么长时间看他博文所获得的进步。