一、概述
与栈相反,队列是先进先出(FIFO),后进后出的数据结构。插入的一端叫做队尾,而出去的一端则称为队头或队首。但是队列(Queue)有一种扩展形式,称为双端队列(Deque),即可以在两端都进行插入和删除的操作,看起来双端队列似乎更加使用,但在实际应用中却并不常见。同样的,队列也有两种实现形式,即顺序队列和链队列。链队列可以参考链栈,直接将出栈操作改成删除头节点即可,插入删除方便,适合栈和队列。
顺序队列当然是数组实现,顺序队列的问题在于出队时前面空出的位置是否由后面的元素补充,如果不补充,那么会造成空间极度的浪费,如果补充,那么需要将每个元素都向前移,时间复杂度此时来到O(N),为了解决这个问题,循环队列应运而生,即将补充的元素放到前面由于出队而造成的空缺位置。这样就可以最大限度的利用已申请的空间。
二、顺序实现循环队列
数据域:
private int Capacity; private int front; private int rear; private int [] data; static int DEFAULT_SIZE = 6; public Queue() { front = rear = 0; Capacity = DEFAULT_SIZE; data = new int [Capacity]; }
由于JAVA并不支持泛型数组,因此我们以int型的队列作为示例。
这里简单描述一下循环队列的结构,一个空的循环队列如下图:

当入队3个元素时变为:
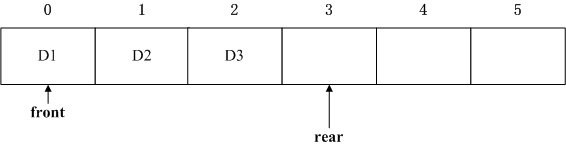
再出队1个元素

接下来是求长度和判满空
public int getSize() { return (rear - front + Capacity) % Capacity; } public boolean isEmpty() { return (rear == front); } public boolean isFull() { return ((rear + 1) % Capacity == front); }
先说求元素个数(长度),从图中看起来好像直接返回rear-front即可,但是因为是循环队列,考虑下列情况:
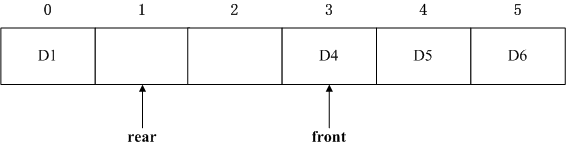
显然不能用简单的减法,必须将两种算法统一起来,因此(rear - front + Capacity) % Capacity正是起到这样的作用。
再看判满,如果将元素完全装满,情况机会变为
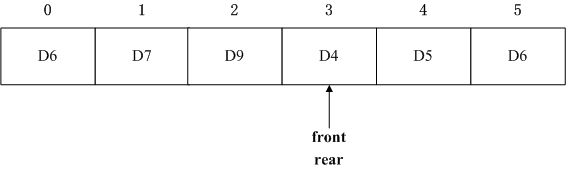
与空的情况一样都是两者重合,因此不能使用front==rear同时判断满和空,官方处理这种情况有两种办法,一是设置Flag进行标记,二是认为还剩一个空位时就认为队列已满。
这里我们采用第二种策略。即下面的情况表示队列已满,请扩容再进行插入,不要完全占满。
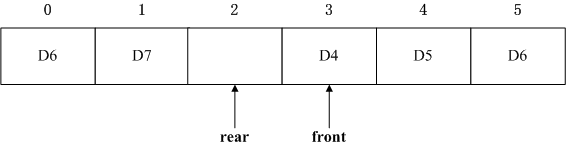
接下来分析入队出队
出队比较简单,只需判断队列是否为空,如果不为空则将front向前移一位(注意front处于末尾怎么移)。
入队则稍微比较复杂,首先判断是否满,如果不满,将新数据赋给当前rear所在的位置,然后rear将向后移一位(注意)。如果队列满了,则需进行扩容,乍一想,好像非常困难(我比较菜),后来仔细一想,你不需要再考虑旧队列的排列,直接相当于一次遍历并按顺序赋给新队列。以下为扩容代码:
public void Enlarge()
{
int newCapacity = Capacity * 2 + 1;
int [] newData = new int [newCapacity];
for (int i = front, j = 0; i != rear; j++, i = (i + 1) % Capacity)
{
newData[j] = data[i];
}
front = 0;
rear = getSize();
data = newData;
Capacity = newCapacity;
}
完整的数据结构代码及主函数测试代码可以查看我的github