链表和二叉查找树的c语言实现

复习数据结构时，手撕的链表和二叉查找树。
我觉得需要解释一下的地方，我都在代码处写了注释。

一.链表

由一个个指针节点链接而成，具体请看下图

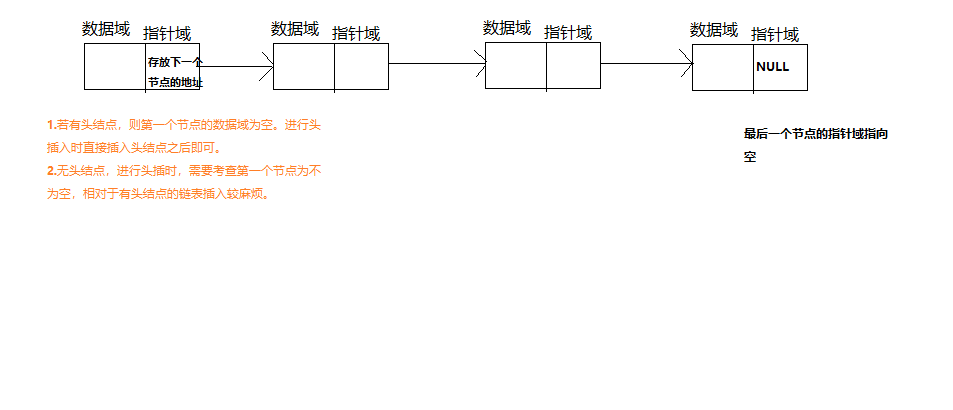
我下面的所有讲解和代码都是基于无头结点的链表，下面对无头结点的链表的操作，仅代表我个人观点，不是只有这一种实现方式。

1.插入

1).头插

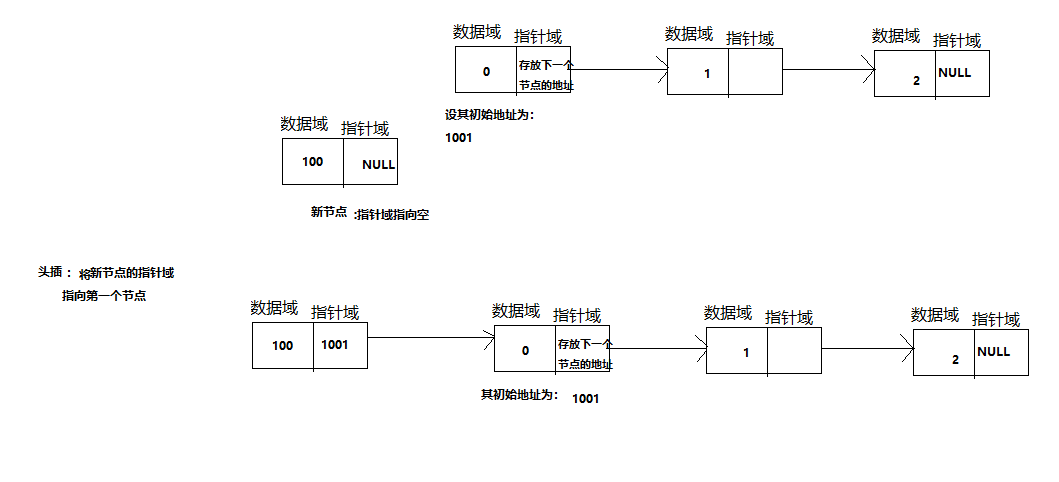
2).尾插

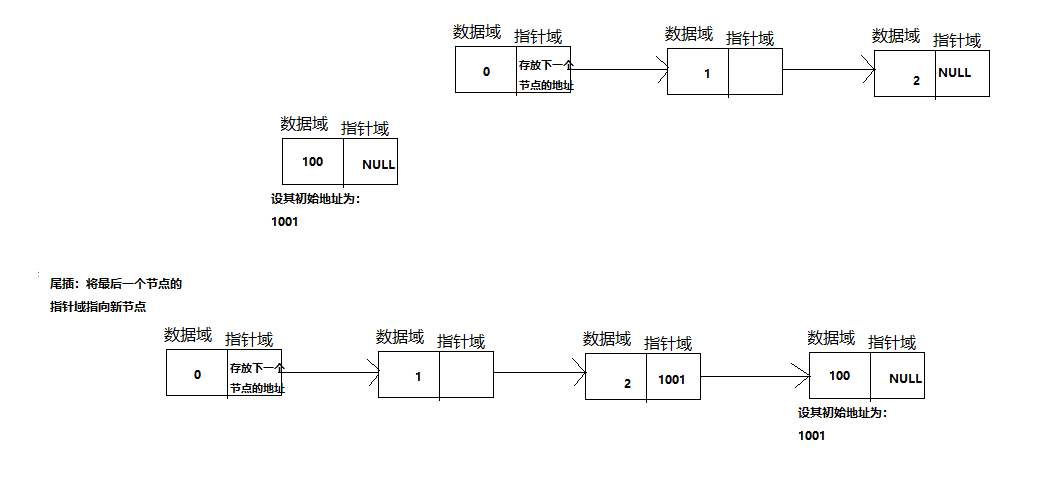
3).在链表中间插入

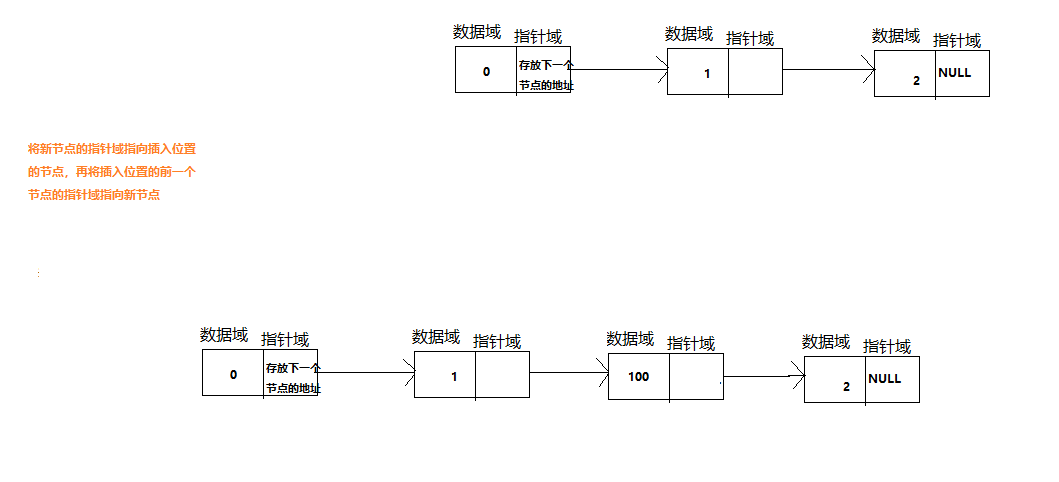
2.删除

删除和插要进行的操作差不多，我就不画图了，画的挺累的。
1).删除第一个节点
保存第一个节点，然后令第一个节点等于它的下一个节点即可(将它覆盖),再释放保存的第一个节点所申请的空间。
2).删除最后一个节点
保存最后一个节点，然后令最后一个节点的前一个节点的指针域指向空,再释放保存的最后一个节点所申请的空间。
3).删除中间的节点
遍历包要删除节点的头一个节点，保存要删除的节点，然后令要删除节点的头一个节点的指针域指向要删除节点的下一个节点(还是把要删除节点覆盖),再释放保存的节点所申请的空间。

#include<bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
typedef struct node{
    int x;
    node *next;
}LNode,*LinkList;

//去重的二叉查找树
typedef struct tnode{
    int x,count;
    tnode *lchild,*rchild;
}TNode,*Tree;

typedef struct lnode{
    Tree Nnode;
    lnode *next;
}Ltnode,*LinktList;

//链表基本操作,无头结点
//已测试，基本功能实现
void LinkList_Head_Insert(LinkList &head,int value){
    if(head->x==inf){//如果root结点为空,直接赋给root
        head->x=value;
        head->next=NULL;
    }
    else{//否则，新建一个节点
        LinkList p;
        p=(LNode*)malloc(sizeof(LNode));
        p->x=value;
        p->next=head;//将它的下一个指向第一个节点的地址
        head=p;//将head指针指向p节点所在地址
    }
}
void LinkList_Tail_Insert(LinkList &tail,int value){//代码功能大致同上
    if(tail->x==inf){
        tail->x=value;
        tail->next=NULL;
    }
    else{
        LinkList p;
        p=(LNode*)malloc(sizeof(LNode));
        p->next=NULL;
        p->x=value;
        tail->next=p;
        tail=p;
    }
}
void LinkList_foreach(LinkList head){
    cout<<"-----"<<endl;
    LinkList p=head;
    int j=1;
    while(p){
        cout<<p->x<<" j="<<j<<endl;
        j++;
        p=p->next;
    }
}
int LinkList_query_byIndex(LinkList &head,int index){
    LinkList p=head;
    int ans,j=1;
    while(p){
        if(j==index){//找到要查询的节点
            ans=p->x;
            break;
        }
        p=p->next;
    }
    return ans;
}
LinkList LinkList_query_byValue(LinkList &head,int value){
    LinkList p=head,q;
    while(p){//遍历链表
        if(p->x==value){
            q=p;
            break;
        }
        p=p->next;
    }
    return q;//返回查找的节点的指针
}
void LinkList_delete_byIndex(LinkList &head,int index){
    LinkList p=head,q;
    int j=1;
    if(index==1){//如果要删除的节点是第一个节点,则直接删除即可
        q=p;
        head=head->next;
        free(q);
        return;
    }
    while(p){
        if(j==index-1){
            break;
        }
        p=p->next;
        j++;
    }
    q=p->next;
    p=p->next->next;
    free(q);
}
void LinkList_delete_byValue(LinkList &head,int value){
    LinkList p=head,q,ppre;
    while(p){
        if(p->x==value)
            break;
        ppre=p;//要删除节点的前一个节点
        p=p->next;
    }
    if(p==head){
        q=head;
        head=head->next;
    }
    else{
        q=p;
        ppre->next=ppre->next->next;
    }
    free(q);
}
//------
//二叉查找树,已测试
void Tree_Insert(Tree &root,int value){
    if(root->x==inf){
        root->x=value;
        root->count=1;
    }
    else{
        Tree p=root;
        while(p){
            if(value>p->x){//要插入的值大于当前节点的值，
            //若当前节点的右子树为空，则新建一个节点，将当前节点的右子树指向新节点
            //否则，令当前节点等于它的右子树，循环继续
                if(p->rchild!=NULL)
                    p=p->rchild;
                else{
                    Tree q;
                    q=(TNode*)malloc(sizeof(TNode));
                    q->rchild=q->lchild=NULL;
                    q->count=1;
                    q->x=value;
                    p->rchild=q;
                    break;
                }
            }
            else if(value<p->x){
                if(p->lchild!=NULL)
                    p=p->lchild;
                else{
                    Tree q;
                    q=(TNode*)malloc(sizeof(TNode));
                    q->rchild=q->lchild=NULL;
                    q->count=1;
                    q->x=value;
                    p->lchild=q;
                    break;
                }
            }
            else{//要插入的值已经在二叉查找树中
                p->count++;
                break;
            }
            
        }
    }
}
int Tree_delete(Tree &root,int value){
    if(root->x==inf){
        return -1;
    }
    else{
        Tree p=root,q,ppre=root;
        int f=0;//0:lchid  1:rchild
        while(p){//查找要删除的节点
            if(value>p->x){
                if(p->rchild!=NULL){
                    ppre=p;//记录要删除节点的根节点
                    p=p->rchild;
                    f=1;
                }
                else
                    return -1;
            }
            else if(value<p->x){
                if(p->lchild!=NULL){
                    ppre=p;
                    p=p->lchild;
                    f=0;
                }
                else
                    return -1;
            }
            else{//找到了要删除的节点
                // 二叉查找树的删除
                q=p;
                if(p->lchild==NULL){//左子树为空，则直接令要删除的节点等于它的右子树
                    p=p->rchild;
                }
                else if(p->rchild==NULL){//右子树为空，则直接令要删除的节点等于它的左子树
                    p=p->lchild;
                }
                else{//如果两个都不为空，新定义两个节点l,r将p=r;然后将l当做一个新节点插入到r中
                    Tree l=p->lchild,r=p->rchild;
                    p=p->rchild;
                    while(r){
                        if(l->x>r->x){
                            if(r->rchild!=NULL)
                                r=r->rchild;
                            else{
                                r->rchild=l;
                                break;
                            }
                        }
                        if(l->x<r->x){
                            if(r->lchild!=NULL)
                                r=r->lchild;
                            else{
                                r->lchild=l;
                                break;
                            }
                        }
                        // if(l->x==r->x),不可能出现这种情况，已经去重
                    }
                }
                if(ppre==root){
                    root=p;
                }
                else{
                    if(f)
                        ppre->rchild=p;
                    else
                        ppre->lchild=p;
                }
                free(q);
                return 1;
            }
            
        }
    }
}
void Tree_query(Tree &root){//TODO:不想写~_~
    ;
}
void LinktList_insert(LinktList &tail,Tree p){
    if(tail==NULL){
        tail->Nnode=p;
        tail->next=NULL;
    }
    else{
        LinktList q;
        q = (Ltnode*)malloc(sizeof(Ltnode));
        q->Nnode=p;
        q->next=NULL;
        tail->next=q;
        tail=q;
    }
}
void Tree_foreach(Tree root){//层序遍历
    Tree p;
    LinktList head,tail,mid_p;//手写队列(命名命错了，懒得改了)
    head=(Ltnode*)malloc(sizeof(Ltnode));
    head->Nnode=root;
    head->next=NULL;
    tail=head;
    while(head){
        p=head->Nnode;
        if(p->lchild!=NULL){
            LinktList_insert(tail,p->lchild);
            // cout<<"l:"<<p->lchild->x<<endl;
        }
        if(p->rchild!=NULL){
            LinktList_insert(tail,p->rchild);
            // cout<<"r:"<<p->rchild->x<<endl;
        }
        mid_p=head;
        head=head->next;
        cout<<p->x<<"  count="<<p->count<<endl;
        free(mid_p);
    }
}


int main(){
    //链表
    LinkList head,tail;
    Tree root;
    head=(LNode*)malloc(sizeof(LNode));
    head->next=NULL;
    head->x=inf;
    tail=head;
    /*
    链表测试代码
    LinkList_Tail_Insert(tail,20);
    LinkList_Head_Insert(head,10);
    LinkList_Tail_Insert(tail,30);
    LinkList_Tail_Insert(tail,40);
    cout<<LinkList_query_byIndex(head,1)<<endl;
    cout<<LinkList_query_byValue(head,20)->x<<endl;    
    LinkList_foreach(head);
    LinkList_delete_byIndex(head,1);
    LinkList_delete_byValue(head,30); 
    LinkList_foreach(head);
    */
    //二叉树
    root = (TNode*)malloc(sizeof(TNode));
    root->lchild=root->rchild=NULL;
    root->x=inf;
    /*
    Tree_Insert(root,20);
    Tree_Insert(root,10);
    Tree_Insert(root,50);
    Tree_Insert(root,30);
    cout<<"---------------------"<<endl;
    Tree_foreach(root);
    Tree_delete(root,20);
    cout<<"--------"<<endl;
    Tree_foreach(root);
    */
   free(root);
   free(head);
    return 0;
}

如有错漏，欢迎指正。