前言：进行之前需要安装SPSS，office 2013。
2.1 名词解释
2.1.1 直方图（Histogram）
2.1.2 数据计量尺度
指对计量对象量化时采用的具体标准，它分为四类：定类尺度、定序尺度、定距尺度和定比尺度。
2.1.3 集中趋势
2.1.4 离中趋势
2.1.5 偏态
数据分布的不对称性称作偏态。
2.1.6 峰度
峰度是指数据分布的尖鞘程度或峰凸程度。
2.2 数据的计量尺度
数据的计量尺度一览表
|
名称
|
逻辑与数学运算
|
常见例子
|
数据类型
|
| 定类尺度 | 等于、不等于 | 性别、民族、职业 |
定性数据
|
| 定序尺度 | 等于、不等于、大于、小于 | 职称、健康状况、质量等级 |
定性数据
|
| 定距尺度 |
等于、不等于、大于、小于
加法、减法
|
年份、摄氏温度、纬度 |
定量数据
|
| 定比尺度 |
等于、不等于、大于、小于
四则运算
|
质量、长度、能量 |
定量数据
|
2.3 数据的集中趋势
2.3.1 定量数据：平均数
平均数是概括数据的一个强有力的方法，它通过消除极端数据的差异将大量的数据浓缩成一个数据来概括，可以较好地实现数据集中趋势的度量，但这种过度的 浓缩使其存在容易受极端值影响的缺点。
比如数列1，2，2，3直方图面积的50%在平均数2的左边，50%在平均数的右边，每一个数占25%的频率。但当改变数列中最后一值，3变为5或者7 。由于 每个数的频率为0.25，因此最后一个的变化不会影响数的频率，但由于数据值的变化，使得平均数发生了变化。
平均数随极端值的变化而变化，而且有向极端值靠近的趋势，因此平均数容易收到极端值的影响。
一组数据按大小顺序排列后，处在数列中点位置的数值，称为中位数。中位数从中间一个点将全部数据分为两部分。
中位数主要用于测试顺序数据的集中趋势，当然也适用于作为定量数据的集中趋势，但不适合分类数据。
中位数的计算：
1.当n为奇数，中位数等于(n+1)/2个数对应的值。
2.当n为偶数，中位数等于n/2和n/2+1的两个数的平均值。
中位数是一个位置代表值，其特点是不受极端值的影响，在分析收入分配等数据时很有用。
2.3.3 分类数据：众数
它主要适用于分类数据，当然也适用于顺序数据和定量数据。一般只有在数据量较大的情况下，众数才有意义。
众数是指一组数据中出现次数最多的变量值。其主要特点是不受极端值的影响，但在一组数据中众数不唯一，有可能有多个众数或者没有众数。
2.4 数据的离中趋势
2.4.1 极差
极差也叫全距，是一组数据中的最大值和最小值的差距。公式表示为：极差= 最大值-最小值如果统计数据已经整理过，并形成组距数列，则极差的近视值为： 极差= 最大组的上限-最小组的下限
极差是测定离中趋势的一种简便方法，它能说明数据组中各数据值的最大变动范围，但由于它根据数据组的两个极端值进行计算的，没有考虑到中间值的变动情 况，所以不能充分反映数据组各项数据的离中趋势，只是一个较粗糙的测定数据离中趋势的指标。
在实际应用中，极差可用于粗略检查产品质量稳定性和进行质量控制。因为在正常生产的条件下，产品质量比较稳定，误差总在一定范围内波动。如有不正常情 况，误差将会超出一定范围。利用极差有助于及时发现问题。
2.4.2 分位距
分位距是全距的一种改进，它是从一组数据中剔除了一部分极端值后重新计算的类似于全距的指标。（四分位距、八分位距、十分位距）
四分位距是第三个四分位数减去第一个四分位数的差的一半。它排除了数列两端各25%单位标志值的影响，反映了数据组中间部分各变量值的最大数与最小数 距离中位数的平均离差。
例：计算数列7，6，8，9，8，4，8，6的四分位距。
a、将数列按从小到大排序：4，6，6，7，8，8，8，9
b、分成4等份：4，6 | 6，7 | 8，8 | 8，9
c、第一个四分位数 = (6+6)/2=6 ；第二个四分位数 = (7+8) /2=7.5，第三个四分位数 = (8+8)/2 = 8
d、这组数据的四分位距为：(8-6)/2=1
这种为了消除极端变量值对测定结果影响的方法，在实际生活中也是常用到的。比如在奥运比赛中，去掉评委一个最高分，一个最低分，然后再计算平均值，就 是为了消除极端变量值对选手得分的影响。
2.4.3 平均差
平均差是数据组中各数据值与其算术平均数离差绝对值的算数平均数，常用符号“M.D”表示。
普通平均差计算：![]()
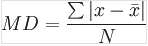
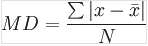
加权平均差计算：![]()
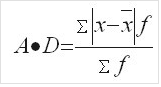
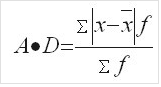
平均差是反映各标志值与算术平均数之间的平均差异。平均差越大，表明各标志值与算术平均数的差异程度越大，该算术均数的代表性就越小；平均差越小，表 明各标志值与算术平均数的差异程度越小，该算术平均数的代表性就越大。当变量数列是由没有分组的数据组或分组后每组的次数相等的数据组成时采用。
例：设某车间有两个班组，各有10名工人，其日产量如下表（表2.5.3）：
|
甲组
|
4
|
7
|
11
|
14
|
14
|
16
|
17
|
24
|
25
|
28
|
|
乙组
|
7
|
12
|
14
|
14
|
15
|
17
|
17
|
19
|
20
|
25
|
甲组的平均值为：（4+7+11+14+14+16+17+24+25+28）/10=16
乙组的平均值为：（7+12+14+14+15+17+17+19+20+25）/10=16
则两组工人日产量的平均差计算过程如下：
|
甲组
|
乙组
|
|
日产量
|
离差
|
离差绝对值
|
日产量
|
离差
|
离差绝对值
|
|
x
|
|
|
x
|
||
|
4
7
11
14
14
16
17
24
25
28
|
-12
-9
-5
-2
-2
0
1
8
9
12
|
12
9
5
2
2
0
1
8
9
12
|
7
12
14
14
15
17
17
19
20
25
|
-9
-4
-2
-2
-1
1
1
3
4
9
|
9
4
2
2
1
1
1
3
4
9
|
|
合计
|
|
60
|
|
|
36
|
两组工人的平均差为：
甲组平均差= 60/10 = 6
乙组平均差= 36/10 = 3.6
也就是说，在甲，乙两组工人平均日产量相同的情况下，甲组数据的离散程度比乙组更大。
由于平均差是根据数列中所有数值计算出来的，受极端值影响较小，所以对整个统计数列的离中趋势有比较充分的代表性。
方差是数据组中各数据值与其算术平均数离差平方的算术平均数。方差的平方根就是标准差。
以表2.5.3为例，计算标准差如下：
|
甲组
|
乙组
|
|
日产量
|
离差
|
离差平方
|
日产量
|
离差
|
离差平方
|
|
x
|
()²
|
x
|
|
()²
|
|
|
4
7
11
14
14
16
17
24
25
28
|
-12
-9
-5
-2
-2
0
1
8
9
12
|
144
81
25
4
4
0
1
64
81
144
|
7
12
14
14
15
17
17
19
20
25
|
-9
-4
-2
-2
-1
1
1
3
4
9
|
81
16
4
4
1
1
1
9
16
81
|
|
合计
|
|
548
|
|
|
214
|
两组的平均差为：
甲组：7.40
已组：4.63
结论可看出，甲，乙两组工人平均日产量相等的情况下，甲的标准差比乙大，所以其平均数的代表性比乙小。
标准差的实质与平均差基本相同，只是在数学处理方法上与平均差不同，平均差是用取绝对值的方法消除离差的正负号然后用算术平均的方法求出平均离差；而 标准差是用平方的方法消除离差的正负号，然后对离差的平方计算算术平均数，并开放求出标准差。即克服了平均差消除正负号带来的弊病，又增加了指标本身 的“灵敏度”，这些有点，使他成为各种离中趋势指标中的重要一种。
标准差的性质：
a，标准差度量了偏离平均数的大小。
b，标准差是一类平均偏差。
c，标准差指出了数列中的数离它们的平均数有多远。数列大多数项离开平均数大约1个σ。极少数项将离开2个或3个σ以上。一般来讲，一个数列中约68%的项 在离平均数的1个σ范围内，其余的32%离的较远。约95%的数据在距平均数的2个σ范围内，其余的5%则较远。
2.4.5 离散系数
极差、平均差、标准差都是对数据的离中趋势进行绝对或平均差异的测定。在通常情况下，它们都带有计量单位，而且其离中趋势大小与变量平均水平的高低有 关。因此，要比较数据平均水平不同的两组数据的离中程度的大小，就有必要计算它们的相对离中程度指标，即离散系数。
常用的是标准差系数，用CV(Coefficient of Variance)表示
用公式表示为：CV=σ/μ
例：有甲、乙两班同时参加统计学原理的课程测试，甲班平均成绩为70分，标准差为9.0分，乙班的成绩如下
|
按成绩分组（分）
|
学生人数（人）
|
|
60以下
60~70
70~80
80~90
90~100
|
2
6
25
12
5
|
比较甲乙两班哪个班的成绩更有代表性？
解：计算如下（公式难打，截图如下）
2.5 数据分布的测试
在描述性统计中，一组数据的特征除了使用集中趋势和离中趋势来描述外， 还使用其分布的形状来分析。数据分布形态的测度主要是以正态分布为标准进行衡量，曲线以均数为中心，左右对称，曲线两端永远不与横轴相交，曲线的高峰位与正中央，即均数所在的位置。
2.5.1 数据偏态及其测定
通常分为右偏（正偏），左偏（负偏）两种。它们是以对称分布为标准相比较而言的。在对称分布的情况下，平均数、中位数与众数是合二为一的，即![]()
。在偏态分布的情况下，平均数。中位数与众数是分离的。如果众数在左边，平均数在右边，即数据的极端值在右边，数据分布曲线向右延伸，则称为右向偏态。右向偏态，众数的数值越小，平均数的数值越大，平均数与众数之差为正值，所以右向偏态又称正向偏态。相反即为左向偏态（负向偏态）。
测定偏态的指标是偏态系数。偏态系数（SK）是对数据分布的不对称性（偏斜程度）的测度。偏态系数有多种计算方法，常用以下公式（s表示样本标准差）：
根据数据计算出SK后，SK含义如下
SK=0，分布是对称的。
SK<0，分布呈负偏态，SK值越小，负偏程度越高。
SK>0，分布呈正偏态，SK值越大，正偏程度越高。
2.5.2 数据峰度及其测定
根据变量值的集中与分散程度，峰度一般表现为三种形态：尖顶峰度、平顶峰度和标准峰度。当变量值的次数在众数周围分布比较集中，使次数分布曲线比正态分布曲线顶峰更为隆起尖峭，称为尖顶峰度；当变量值的次数在众数周围分布为分散，使次数分布曲线较正态分布曲线更为平缓，称为平顶峰度。
测定峰度的指标是峰度系数。峰度系数（K）是对数据分布的尖峭程度的测度。峰度系数有多种计算方法，常用公式如下：
根据计算出K后，K的含义如下。
K<0，呈平顶峰度。
K>0，呈尖顶峰度。
2.5.3 数据偏度和峰度的作用
在实际的数据分析过程中，偏度和峰度的作用主要表现在以下两个方面。
一是将偏度和峰度结合起来检查样本的分布是否属于正态分布，以便判断总体的分布。如果样本偏度接近于0而峰度接近于3，就可以判断总体分布是接近于正态分布的，用样本来对总体进行测定时就可以看成是正态分布，否则就可以进行否认。
二是利用资料之间存在的偏度关系，对算术平均数、众数、中位数进行推算。一般情况下，只要分布不是正态的，算术平均数。众数、中位数之间都存在以下关系。
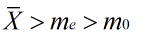
右偏时：
![]()
；左偏时：![]()
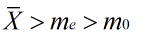
在偏度适度时，不论右偏还是左偏，三者间的距离有近似的固定关系，即中位数与算术平均数的距离，约等于众数与算术平均数距离的1/3。可得以下关系式：
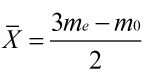
2.6 数据的展示-统计图
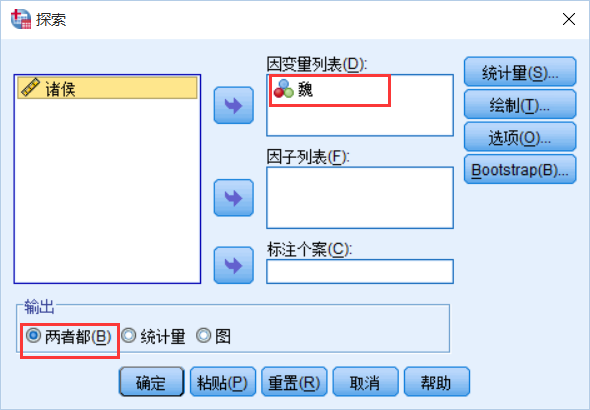
2.6.1 SPSS画统计图
录入数据
2.6.2 Excel画统计图
感谢您的支持与关注！