题意
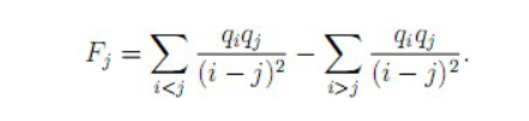
求解 Ei = Fi/qi
解法:
方法一:
考虑左侧的式子,直接多项式乘法。
对于右面的式子,我们记做$B_j$,这样有
$$B_j = sum_{j<i}{ revq_{n-i} f(i-j) }$$
$$B_j = sum_{0<k<n-j}{ revq_t f(n-j-t) }$$
$$B_j = (revq otimes f)_{n-j}$$
五次DFT变形即可。
在卡精度的情况下可以用实时用三角函数算 $wt$ 代替用 $wn$ 连乘旋转得到 $wt$。

#include <bits/stdc++.h> #define PI acos(-1) const int N = 100010; using namespace std; struct EX { double real,i; EX operator+(const EX tmp)const{return (EX){real+tmp.real, i+tmp.i};}; EX operator-(const EX tmp)const{return (EX){real-tmp.real, i-tmp.i};}; EX operator*(const EX tmp)const{return (EX){real*tmp.real - i*tmp.i, real*tmp.i + i*tmp.real};}; }; int R[N<<2]; void DFT(EX a[],int n,int tp_k) { for(int i=0;i<n;i++) if(i<R[i]) swap(a[i],a[R[i]]); for(int d=1;d<n;d<<=1) { EX wn = (EX){cos(PI/d), sin(PI/d)*tp_k}; for(int i=0;i<n;i += (d<<1)) { EX wt = (EX){1,0}; //高速度用 for(int k=0;k<d;k++, wt = wt*wn) { // EX wt = (EX){cos(PI*k / d) ,tp_k*sin(PI*k / d)}; //高精度用(到 10^14 的精度) EX A0 = a[i+k], A1 = wt * a[i+k+d]; a[i+k] = A0+A1; a[i+k+d] = A0-A1; } } } if(tp_k==-1) for(int i=0;i<n;i++) a[i] = (EX){a[i].real/n, a[i].i/n}; } int n,m; EX A[N<<2],B[N<<2],C[N<<2]; double q[N],ans[N]; int main() { freopen("force.in", "r", stdin); freopen("force.out", "w", stdout); scanf("%d",&n); for(int i=0;i<n;i++) scanf("%lf",&q[i]); int L = 0,tot; while((1<<L)<n+n-1) L++; tot = (1<<L); for(int i=1;i<tot;i++) R[i]=(R[i>>1]>>1)|((i&1)<<(L-1)); for(int i=0;i<n;i++) A[i] = (EX){q[i], 0}; for(int i=1;i<n;i++) B[i] = (EX){1/(double)i/(double)i, 0}; DFT(A,tot,1); DFT(B,tot,1); for(int i=0;i<tot;i++) C[i] = A[i]*B[i]; DFT(C,tot,-1); for(int i=0;i<n;i++) ans[i] += C[i].real; memset(A,0,sizeof(A)); for(int i=1;i<n;i++) A[i] = (EX){q[n-i], 0}; DFT(A,tot,1); for(int i=0;i<tot;i++) C[i] = A[i]*B[i]; DFT(C,tot,-1); for(int i=0;i<n;i++) ans[i] -= C[n-i].real; for(int i=0;i<n;i++) printf("%.3lf ",ans[i]); return 0; }
方法二:
考虑拓展
$$C_{j+n} = sum_{0 leq k leq j+n} { q_k A_{j+n-k} }$$
其中
$A_i = frac{1}{(i-n)^2} (n < i < 2n)$
$A_i = frac{1}{(n-i)^2} (0 < i < n)$
从而有 $B_j = C_{j+n}$
其他全为0,这样一次FFT卷积得到答案

#include <bits/stdc++.h> #define PI acos(-1) const int N = 100010; using namespace std; struct EX { double real,i; EX operator+(const EX tmp)const{return (EX){real+tmp.real, i+tmp.i};}; EX operator-(const EX tmp)const{return (EX){real-tmp.real, i-tmp.i};}; EX operator*(const EX tmp)const{return (EX){real*tmp.real - i*tmp.i, real*tmp.i + i*tmp.real};}; }; int R[N<<3]; void DFT(EX a[],int n,int tp_k) { for(int i=0;i<n;i++) if(i<R[i]) swap(a[i],a[R[i]]); for(int d=1;d<n;d<<=1) { EX wn = (EX){cos(PI/d), sin(PI/d)*tp_k}; for(int i=0;i<n;i += (d<<1)) { EX wt = (EX){1,0}; //高速度用 for(int k=0;k<d;k++, wt = wt*wn) { // EX wt = (EX){cos(PI*k / d) ,tp_k*sin(PI*k / d)}; //高精度用(到 10^14 的精度) EX A0 = a[i+k], A1 = wt * a[i+k+d]; a[i+k] = A0+A1; a[i+k+d] = A0-A1; } } } if(tp_k==-1) for(int i=0;i<n;i++) a[i] = (EX){a[i].real/n, a[i].i/n}; } int n,m; EX A[N<<3],B[N<<3],C[N<<3]; double q[N],ans[N]; int main() { freopen("force.in", "r", stdin); freopen("force.out", "w", stdout); scanf("%d",&n); for(int i=0;i<n;i++) scanf("%lf",&q[i]); int L = 0,tot; while((1<<L)<4*n-1) L++; tot = (1<<L); for(int i=1;i<tot;i++) R[i]=(R[i>>1]>>1)|((i&1)<<(L-1)); for(int i=0;i<n;i++) A[i] = (EX){q[i], 0}; for(int i=1;i<n;i++) { B[i] = (EX){-1/(double)(n-i)/(double)(n-i), 0}; B[i+n] = (EX){1/(double)i/(double)i, 0}; } DFT(A,tot,1); DFT(B,tot,1); for(int i=0;i<tot;i++) C[i] = A[i]*B[i]; DFT(C,tot,-1); for(int i=0;i<n;i++) ans[i] = C[i+n].real; for(int i=0;i<n;i++) printf("%.3lf ",ans[i]); return 0; }
