meeting：给正n边形每个点染上黑色或者白色，问有多少个同色的等腰三角形。
以正五边形为例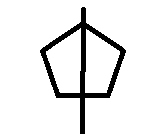
这里将最上面的点作为顶点，得到若干对相等的腰
，注意到以最上面的点作为顶点的等腰三角形的个数，等于颜色相等且都为顶点颜色的对称点的个数。
O(n^2)统计即可。
PS：注意减去等边三角形的情况。
1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 #include <cstdlib> 5 #include <ctime> 6 #include <cmath> 7 #include <algorithm> 8 #include <set> 9 #include <map> 10 #include <queue> 11 12 #define N 1000010 13 #define LL long long 14 15 using namespace std; 16 17 int n, cnt0[2], cnt1[2]; 18 char S[N]; 19 20 int pos(int i){ //i做镜像操作后的位置 21 if(i==0) return i; 22 return n-i; 23 } 24 25 LL calc0(){ 26 if(n <= 2) return 0; 27 LL ans = 0; 28 for(int s=0;s<n;s++) { 29 int tmp = 0; 30 for(int i=0, j=s;i<n;i++) { 31 if(S[i] == S[s] && S[pos(j)] == S[s]) { 32 if(i != s && pos(j) != i && pos(j) != s) ans ++; 33 else if((i == s || pos(j) == s) && pos(j) != i) tmp ++; 34 } 35 cout << i << " match " << j << endl; 36 j = (j-2+n)%n; 37 } 38 cout << endl; 39 // cout << n << " tmp = " << tmp << endl; 40 } 41 ans/=2; 42 return ans; 43 } 44 45 LL calc_ex(){ 46 if((n-3) % 3 != 0) return 0LL; 47 int ans = 0; 48 int t = n/3; 49 for(int i=0;i<n;i++) 50 if(S[i] == S[(i+t)%n] && S[i] == S[(i+2*t)%n]) ans ++; 51 return (ans/3LL) * 2LL; 52 } 53 54 int main() { 55 freopen("test.txt","r",stdin); 56 int T; 57 scanf("%d",&T); 58 while(T--) { 59 scanf("%s",S); 60 n=strlen(S); 61 //cout << calc0() << endl; 62 cout << calc0()-calc_ex() << endl; 63 } 64 return 0; 65 }
POJ3659：新颖的题目，有一个长度为n的整数序列，数字两两不同，给出m个Li到Ri最小值为vi的命题，问到第几个最先出现冲突。
首先，二分是必然的，接下来就考虑如何判定二分出的若干个命题是否冲突。
Li到Ri最小值为vi 等价于 对于j∈[Li,Ri] 有aj >= vi，且必然存在aj = vi。
从而将命题按vi从大到小排序，并对于所有vi相同的区间算出 [L交,R交]，冲突一定出在
1.前面的命题和后面的命题冲突（前面的命题限制了所有的aj ∈[L交,R交]，有aj>vi）
2.vi相同的命题冲突（vi相同的区间的交为空）
线段树/并查集即可。
PS：在考虑当前vi相等的区间们 对后面区间们的影响时要考虑并集。
1 #include <cstdio> 2 #include <algorithm> 3 #include <iostream> 4 5 #define l(x) ch[x][0] 6 #define r(x) ch[x][1] 7 #define LL long long 8 9 const int N = 200010; 10 11 using namespace std; 12 13 struct node{ 14 int l,r,v; 15 }a[N],b[N]; 16 17 int totn,n,m,a0[N<<1]; 18 int ch[N<<1][2],setv[N<<1],minv[N<<1]; 19 20 int build(int l,int r){ 21 int x=++totn; 22 minv[x]=setv[x]=0; 23 if(l==r) return x; 24 int mid=(l+r)>>1; 25 l(x)=build(l,mid); 26 r(x)=build(mid+1,r); 27 return x; 28 } 29 30 void update(int x){ 31 minv[x] = min(minv[l(x)],minv[r(x)]); 32 } 33 34 void push(int x,int l,int r){ 35 if(!setv[x]) return; 36 setv[l(x)] = max(setv[l(x)],setv[x]); 37 setv[r(x)] = max(setv[r(x)],setv[x]); 38 minv[l(x)] = max(minv[l(x)],setv[x]); 39 minv[r(x)] = max(minv[r(x)],setv[x]); 40 setv[x]=0; 41 } 42 43 int qmin(int x,int l,int r,int ql,int qr){ 44 push(x,l,r); 45 if(ql<=l && r<=qr) return minv[x]; 46 int mid=(l+r)>>1,ans=0x3f3f3f3f; 47 if(ql<=mid) ans = min(ans,qmin(l(x),l,mid,ql,qr)); 48 if(mid<qr) ans = min(ans,qmin(r(x),mid+1,r,ql,qr)); 49 update(x); 50 return ans; 51 } 52 53 void change(int x,int l,int r,int ql,int qr,int qv){ 54 push(x,l,r); 55 if(ql<=l && r<=qr){ 56 setv[x]=qv; 57 minv[x]=max(minv[x],qv); 58 return; 59 } 60 int mid=(l+r)>>1; 61 if(ql<=mid) change(l(x),l,mid,ql,qr,qv); 62 if(mid<qr) change(r(x),mid+1,r,ql,qr,qv); 63 update(x); 64 } 65 66 bool cmp(node a, node b){ 67 return a.v>b.v; 68 } 69 70 bool check(int t){ 71 int tot=0; 72 for(int i=1;i<=t;i++) b[++tot]=a[i]; 73 totn=0; 74 build(1,a0[0]); 75 sort(b+1,b+tot+1,cmp); 76 int j=1; 77 while(j<=tot){ 78 int l=b[j].l,r=b[j].r,L=b[j].l,R=b[j].r; 79 while(j<tot && b[j+1].v==b[j].v){ 80 l =max(l,b[j+1].l); 81 r =min(r,b[j+1].r); 82 L =min(L,b[j+1].l); 83 R =max(R,b[j+1].r); 84 j++; 85 } 86 if(l>r) return 0; 87 int tp = qmin(1,1,a0[0],l,r); 88 if(tp>b[j].v) return 0; 89 change(1,1,a0[0],L,R,b[j].v); 90 j++; 91 } 92 return 1; 93 } 94 95 int a1[N]; 96 97 void prework(){ 98 for(int i=1;i<=m;i++) a1[i]=a[i].v; 99 sort(a1+1,a1+m+1); 100 int tot1=1; 101 for(int i=2;i<=m;i++) if(a1[i]!=a1[i-1]) a1[++tot1]=a1[i]; 102 for(int i=1;i<=m;i++) a[i].v = lower_bound(a1+1,a1+tot1+1,a[i].v)-a1; 103 } 104 105 int main(){ 106 // freopen("test.txt","r",stdin); 107 // freopen("mine.out","w",stdout); 108 // puts("error"); 109 scanf("%d%d",&n,&m); 110 // cout<<n<<' '<<m<<endl; 111 a0[0]=0; 112 for(int i=1;i<=m;i++) { 113 scanf("%d%d%d",&a[i].l,&a[i].r,&a[i].v); 114 a0[++a0[0]]=a[i].l; 115 a0[++a0[0]]=a[i].r; 116 } 117 prework(); 118 sort(a0+1,a0+a0[0]+1); 119 int tot0=1; 120 for(int i=2;i<=a0[0];i++) if(a0[i]!=a0[i-1]) a0[++tot0]=a0[i]; 121 a0[0]=tot0; 122 for(int i=2;i<=tot0;i++) if(a0[i]!=a0[i-1]+1) a0[++a0[0]]=a0[i-1]+1; 123 sort(a0+1,a0+a0[0]+1); 124 for(int i=1;i<=m;i++){ 125 a[i].l=lower_bound(a0+1,a0+a0[0]+1,a[i].l)-a0; 126 a[i].r=lower_bound(a0+1,a0+a0[0]+1,a[i].r)-a0; 127 } 128 int l=1,r=m; 129 while(r-l>5){ 130 int mid=(l+r)>>1; 131 if(!check(mid)) r=mid; 132 else l=mid; 133 } 134 for(int i=l;i<=r;i++) 135 if(!check(i)){ 136 printf("%d ",i); 137 return 0; 138 } 139 puts("0"); 140 return 0; 141 } 142 /* 143 20 4 144 1 10 7 145 5 19 7 146 3 12 8 147 11 15 12 148 */
BZOJ4377：题目有些累赘，见官网。
注意到c[i]%n得到0~n-1 。且一一对应。
所以考虑有多少个自序序列等于给定串，相当于考虑有多少个i满足从i开始的m个字符能和给定串匹配。
排除最后的m-1个i，本题相当于问有多少个x，满足
(x + i*a) %n < P (c[i] == 0)
(x + i*a) %n >= P (c[i] == 1)
对于这m个等式，每一个等式可以得到一个不满足条件的x的取值区域。
对这2*m个区间求并取反集就是答案区间。
1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 #include <cstdlib> 5 #include <ctime> 6 #include <cmath> 7 #include <algorithm> 8 #include <set> 9 #include <map> 10 #include <queue> 11 12 #define LL long long 13 #define N 1000010 14 15 using namespace std; 16 17 LL n,a,b,P; 18 int m,tot; 19 char c[N]; 20 21 struct node{ 22 int l,r; 23 }q[3*N]; 24 25 bool cmp(node a,node b){ 26 return a.l<b.l; 27 } 28 29 int main(){ 30 freopen("test.txt","r",stdin); 31 cin>>n>>a>>b>>P>>m; 32 while(!isdigit(c[0]=getchar())); 33 for(int i=1;i<m;i++) c[i]=getchar(); 34 int ans=n; 35 LL tmp; 36 tmp=b%n; 37 for(int i=1;i<m;i++){ 38 tmp=(tmp-a+n) % n; 39 q[++tot] = (node){(int)tmp,(int)tmp}; 40 } 41 for(int i=0;i<m;i++){ 42 LL l,r; 43 if(c[i]=='1') l=-i*a,r=P-1LL-i*a; 44 else l=P-i*a,r=n-1LL-i*a; 45 l=(l%n+n)%n; 46 r=(r%n+n)%n; 47 if(l>r){ 48 q[++tot]=(node){0,(int)r}; 49 q[++tot]=(node){(int)l,(int)(n-1)}; 50 } 51 else q[++tot] = (node){(int)l,(int)r}; 52 } 53 // for(int i=1;i<=tot;i++) cout<<q[i].l<<' '<<q[i].r<<endl; 54 sort(q+1,q+tot+1,cmp); 55 LL l=q[1].l,r=q[1].r; 56 for(int i=2;i<=tot;i++){ 57 if(q[i].l>r){ 58 ans-=(int)(r-l+1); 59 l=q[i].l; 60 r=q[i].r; 61 } 62 else r=max(r,(LL)q[i].r); 63 } 64 ans-=(int)(r-l+1); 65 printf("%d ",ans); 66 return 0; 67 }
hdu5299（待补完博弈论理论），平面上有n个圆，圆与圆互不相切相交，Alice，Bob轮流选圆，每一次删掉选定圆与其包含的所有圆，问是否先手必胜。
每个圆和第一个包含它的圆连边，得到一个森林。
本题博弈论部分是经典模型，关键在于如何建出树来。
首先对于所有的圆，它们的上下关系不会发生变化，所以考虑用set来维护。
将xi-Ri和xi+Ri作为扫描线，x从小到大枚举。
圆在set中的权值 为 圆与当前x的靠上交点的y坐标，这样对于每一个加进来的圆，lowerbound一下就好了。
注意lowerbound到的第一个圆不一定是加进来的圆的father（可能同为子节点），如果不是要一直沿着树向上找，直到找到其father。
这个过程可以二分一下（因为越向上包含当前圆的可能性越大），向上找的过程用倍增就好了。
PS：我懒，写的暴力上翻。
1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 #include <cstdlib> 5 #include <ctime> 6 #include <cmath> 7 #include <algorithm> 8 #include <set> 9 #include <map> 10 #include <queue> 11 12 #define eps 1e-8 13 #define LD double 14 #define sqr(x) ((x)*(x)) 15 #define N 40010 16 #define LL long long 17 18 using namespace std; 19 20 int X; 21 22 struct edge{ 23 int x,to; 24 }E[N]; 25 26 struct node{ 27 int x,y,R; 28 int id; 29 void scan(){ 30 scanf("%d%d%d",&x,&y,&R); 31 } 32 bool operator<(const node &a)const{ 33 LD t0 = sqrt(sqr(R)-(LD)sqr((LD)X-(LD)x)) + (LD)y; 34 LD t1 = sqrt(sqr(a.R)-(LD)sqr((LD)X-(LD)a.x)) + (LD)a.y; 35 if(fabs(t0-t1)<eps) return 0; 36 return t0<t1; 37 } 38 }a[N],b[N],a0[N]; 39 40 set<node> Tp; 41 42 int n; 43 int X0[N<<1]; 44 45 bool cmp1(node a,node b){ 46 return a.x-a.R<b.x-b.R; 47 } 48 49 bool cmp2(node a,node b){ 50 return a.x+a.R<b.x+b.R; 51 } 52 53 int totE,g[N],sg[N],fa[N]; 54 bool vis[N]; 55 56 void ade(int x,int y){ 57 // cout<<"ade "<<x<<' '<<y<<endl; 58 E[++totE]=(edge){y,g[x]}; g[x]=totE; 59 fa[y]=x; 60 } 61 62 #define p E[i].x 63 64 int dfs(int x){ 65 // bool flag=0; 66 // for(int i=g[x];i;i=E[i].to) dfs(p),flag=1; 67 // if(!flag) return sg[x]=0; 68 // for(int i=g[x];i;i=E[i].to) vis[sg[p]]=1; 69 // for(sg[x]=0;vis[sg[x]];sg[x]++); 70 // for(int i=g[x];i;i=E[i].to) vis[sg[p]]=0; 71 // return sg[x]; 72 int ans=0; 73 for(int i=g[x];i;i=E[i].to) ans^=dfs(p)+1; 74 return ans; 75 } 76 77 int main(){ 78 freopen("test.txt","r",stdin); 79 //freopen(".out","w",stdout); 80 int T; 81 scanf("%d",&T); 82 while(T--){ 83 memset(g,0,sizeof(g)); 84 memset(fa,0,sizeof(fa)); 85 totE=0; 86 scanf("%d",&n); 87 for(int i=1;i<=n;i++){ 88 a[i].scan(); 89 a[i].id=i; b[i]=a[i]; 90 a0[i]=a[i]; 91 } 92 X0[0]=0; 93 for(int i=1;i<=n;i++){ 94 X0[++X0[0]]=a[i].x-a[i].R; 95 X0[++X0[0]]=a[i].x+a[i].R; 96 } 97 sort(X0+1,X0+X0[0]+1); 98 int tot=1; 99 for(int i=2;i<=X0[0];i++) 100 if(X0[i]!=X0[i-1]) X0[++tot]=X0[i]; 101 sort(a+1,a+n+1,cmp1); 102 sort(b+1,b+n+1,cmp2); 103 set<node>::iterator it; 104 Tp.clear(); 105 int j=1,k=1; 106 for(int i=1;i<=tot;i++){ 107 X=X0[i]; 108 while(k<=n && b[k].x+b[k].R==X0[i]){ 109 it=Tp.find(b[k]); 110 Tp.erase(it); 111 k++; 112 } 113 while(j<=n && a[j].x-a[j].R==X0[i]){ 114 it=Tp.lower_bound(a[j]); 115 if(it!=Tp.end()){ 116 int t=it->id; 117 while(t){ 118 if(sqr(a0[t].x-(LL)a[j].x)+sqr(a0[t].y-(LL)a[j].y)<sqr((LL)a0[t].R)){ 119 ade(t,a[j].id); 120 break; 121 } 122 t=fa[t]; 123 } 124 } 125 Tp.insert(a[j]); 126 j++; 127 } 128 } 129 int ans=0; 130 for(int i=1;i<=n;i++) if(!fa[i]) ans^=dfs(i)+1; 131 if(ans) puts("Alice"); 132 else puts("Bob"); 133 } 134 return 0; 135 }
hdu5290：一棵树，边权为1，每个点有一个≤100的爆炸半径Ri，如果引爆i点，到i点距离小于等于Ri的点都会被炸掉，问最少引爆多少点，
注意到影响状态的无非要炸的深度和点。
f[i][j]表示爆炸还需要从i点向下传播j层 最少炸的次数（注意j可能为负）
dp即可，O(nm)