JS的基础类型Number,遵循 IEEE 754 规范,采用双精度存储(double precision),占用 64 bit。如图

意义
- 1位用来表示符号位
- 11位用来表示指数
- 52位表示尾数
浮点数,比如
|
1
2
|
0.1 >> 0.0001 1001 1001 1001…(1001无限循环)0.2 >> 0.0011 0011 0011 0011…(0011无限循环) |
此时只能模仿十进制进行四舍五入了,但是二进制只有 0 和 1 两个,于是变为 0 舍 1 入。这即是计算机中部分浮点数运算时出现误差,丢失精度的根本原因。
大整数的精度丢失和浮点数本质上是一样的,尾数位最大是 52 位,因此 JS 中能精准表示的最大整数是 Math.pow(2, 53),十进制即 9007199254740992。
大于 9007199254740992 的可能会丢失精度
|
1
2
3
|
9007199254740992 >> 10000000000000...000 // 共计 53 个 09007199254740992 + 1 >> 10000000000000...001 // 中间 52 个 09007199254740992 + 2 >> 10000000000000...010 // 中间 51 个 0 |
实际上
|
1
2
3
4
|
9007199254740992 + 1 // 丢失9007199254740992 + 2 // 未丢失9007199254740992 + 3 // 丢失9007199254740992 + 4 // 未丢失 |
解决方法:
对于整数,前端出现问题的几率可能比较低,毕竟很少有业务需要需要用到超大整数,只要运算结果不超过 Math.pow(2, 53) 就不会丢失精度。
对于小数,前端出现问题的几率还是很多的,尤其在一些电商网站涉及到金额等数据。解决方式:把小数放到位整数(乘倍数),再缩小回原来倍数(除倍数)
|
1
2
|
// 0.1 + 0.2(0.1*10 + 0.2*10) / 10 == 0.3 // true |
以下摘自百度:
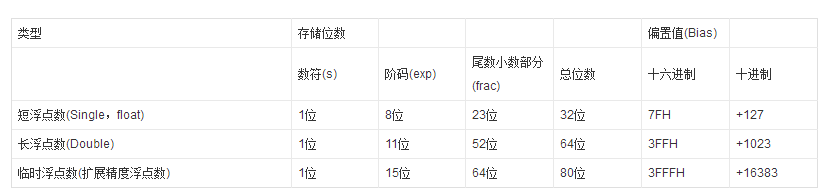
IEEE 754标准规定了什么IEEE 754 规定:
a) 两种基本浮点格式:单精度和双精度。IEEE单精度格式具有24位有效数字,并总共占用32 位。IEEE双精度格式具有53位有效数字精度,并总共占用64位。 说明:基本浮点格式是固定格式,相对应的十进制有效数字分别为7位和17位。基本浮点格式对应的C/C++类型为float和double。
b) 两种扩展浮点格式:单精度扩展和双精度扩展。此标准并未规定扩展格式的精度和大小,但它指定了最小精度和大小。例如,IEEE 双精度扩展格式必须至少具有64位有效数字,并总共占用至少79 位。 说明:虽然IEEE 754标准没有规定具体格式,但是实现者可以选择符合该规定的格式,一旦实现,则为固定格式。例如:x86 FPU是80位扩展精度,而Intel安腾FPU是82位扩展精度,都符合IEEE 754标准的规定。C/C++对于扩展双精度的相应类型是long double,但是,Microsoft Visual C++ 6.0版本以上的编译器都不支持该类型,long double和double一样,都是64位基本双精度,只能用其它C/C++编译器或汇编语言。
c) 浮点运算的准确度要求:加、减、乘、除、平方根、余数、将浮点格式的数舍入为整数值、在不同浮点格式之间转换、在浮点和整数格式之间转换以及比较。求余和比较运算必须精确无误。其他的每种运算必须向其目标提供精确的结果,除非没有此类结果,或者该结果不满足目标格式。对于后一种情况,运算必须按照下面介绍的规定舍入模式的规则对精确结果进行最低限度的修改,并将经过此类修改的结果提供给运算的目标。 说明:IEEE754没有规定基本算术运算(+、-、×、/ 等)的结果必须精确无误,因为对于IEEE 754的二进制浮点数格式,由于浮点格式长度固定,基本运算的结果几乎不可能精确无误。这里用三位精度的十进制加法来说明: 例1:a = 3.51,b = 0.234,求a+b = ? a与b都是三位有效数字,但是,a+b的精确结果为3.744,是四位有效数字,对于该浮点格式只有三位精度,a+b的结果无法精确表示,只能近似表示,具体运算结果取决于舍入模式(见舍入模式的说明)。同理,由于浮点格式固定,对于其他基本运算,结果也几乎无法精确表示。
d) 在十进制字符串和两种基本浮点格式之一的二进制浮点数之间进行转换的准确度、单一性和一致性要求。对于在指定范围内的操作数,这些转换必须生成精确的结果(如果可能的话),或者按照规定舍入模式的规则,对此类精确结果进行最低限度的修改。对于不在指定范围内的操作数,这些转换生成的结果与精确结果之间的差值不得超过取决于舍入模式的指定误差。
说明:这一条规定是针对十进制字符串表示的数据与二进制浮点数之间相互转换的规定,也是一般编程者最容易产生错觉的事情。因为人最熟悉的是十进制,以为对于任意十进制数,二进制都应该能精确表示,其实不然。本文主要目的就是揭密二进制浮点数所能够精确表示的十进制数,如果你以前没有想过这个问题,绝对让你吃惊。卖个关子先!
e) 五种类型的IEEE 浮点异常,以及用于向用户指示发生这些类型异常的条件。五种类型的浮点异常是:无效运算、被零除、上溢、下溢和不精确。
说明:关于浮点异常,见Kahan教授的《Lecture Notes on IEEE 754》,这里我就不浪费口水了。
f) 四种舍入方向:向最接近的可表示的值;当有两个最接近的可表示的值时首选"偶数"值;向负无穷大(向下);向正无穷大(向上)以及向0(截断)。
说明:舍入模式也是比较容易引起误解的地方之一。我们最熟悉的是四舍五入模式,但是,IEEE 754标准根本不支持,它的默认模式是最近舍入(Round to Nearest),它与四舍五入只有一点不同,对.5的舍入上,采用取偶数的方式。举例比较如下:
最近舍入模式:
Round(0.5) = 0;
Round(1.5) = 2;
Round(2.5) = 2;
四舍五入模式:
Round(0.5) = 1;
Round(1.5) = 2;
Round(2.5) = 3;
主要理由:由于字长有限,浮点数能够精确表示的数是有限的,因而也是离散的。在两个可以精确表示的相邻浮点数之间,必定存在无穷多实数是IEEE浮点数所无法精确表示的。如何用浮点数表示这些数,IEEE 754的方法是用距离该实数最近的浮点数来近似表示。但是,对于.5,它到0和1的距离是一样近,偏向谁都不合适,四舍五入模式取1,虽然银行在计算利息时,愿意多给0.5分钱,但是,它并不合理。例如:如果在求和计算中使用四舍五入,一直算下去,误差有可能越来越大。机会均等才公平,也就是向上和向下各占一半才合理,在大量计算中,从统计角度来看,高一位分别是偶数和奇数的概率正好是50% : 50%。至于为什么取偶数而不是奇数,大师Knuth有一个例子说明偶数更好,于是一锤定音。最近舍入模式在C/C++中没有相应的函数,当然,IEEE754以及x86 FPU的默认舍入模式是最近舍入,也就是每次浮点计算结果都采用最近舍入模式,除非用程序显式设置为其它三种舍入模式。 另外三种舍入模式,简要说明。
向0(截断)舍入:
C/C++的类型转换。
(int) 1.324 = 1
(int) -1.324 = -1
向负无穷大(向下)舍入:
C/C++函数floor()。例如:
floor(1.324) = 1
floor(-1.324) = -2
向正无穷大(向上)舍入:
C/C++函数ceil()
ceil(1.324) = 2
Ceil(-1.324) = -1
后两种舍入方法据说是为了数值计算中的区间算法,但很少听说哪个商业软件使用区间算法。