两个数的最大公因数

1.问题描述
给出两个正整数，求他们的最大公约数
2.问题分析
算法1：连续整数检验法（穷举法）
d=min{m,n}
如果m与n能同时整除d，则d是两个数的最大公约数。
否则，若任一条件不成立，d=d-1,直到能同时整除。

 

eg：12与9，将9赋给d,12不能整除9，则d-1为8.

12与9均不能整除8，d=d-1.

直到d=3,12与9都能整除3，则3为12与9的最大公因数。

#include<stdio.h>
int  f(int m,int n){
    int d;
    if(m<n)
    d=m;
    else 
    d=n;
    while(d>0)
    {
        if(m%d==0&&n%d==0)
        return d;
        d--;
    }


}
 
int main()
{
    int m,n;
    printf("请输入两个正整数："); 
    scanf("%d %d",&m,&n);
    printf("这两个数的最大公约数为:%d ",f(m,n));
     
}

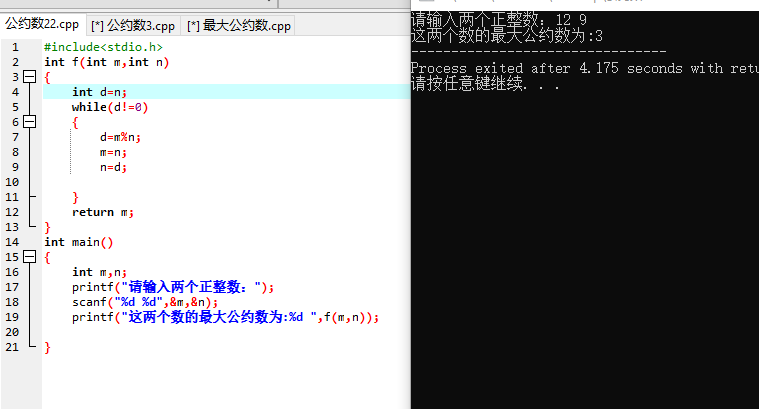
算法2：欧几里得算法
1.d=m%n;
2.循环直到r=0;

   d=m%n;
   m=n;
   n=d;

3.返回m.

 

eg:d为m与n的模。

d=12%9=3;

m=n=9;

n=d=3;

继续循环；

d=9%3=0;

m=n=3;

n=d=0;

跳出循环。返回m值，为最大公因数。

 

#include<stdio.h>
int f(int m,int n)
{
    int d;
    while(d!=0)
    {
        d=m%n;
        m=n;
        n=d;
    
    }
    return m;
}
int main()
{
    int m,n;
    printf("请输入两个正整数："); 
    scanf("%d %d",&m,&n);
    printf("这两个数的最大公约数为:%d ",f(m,n));
     
}

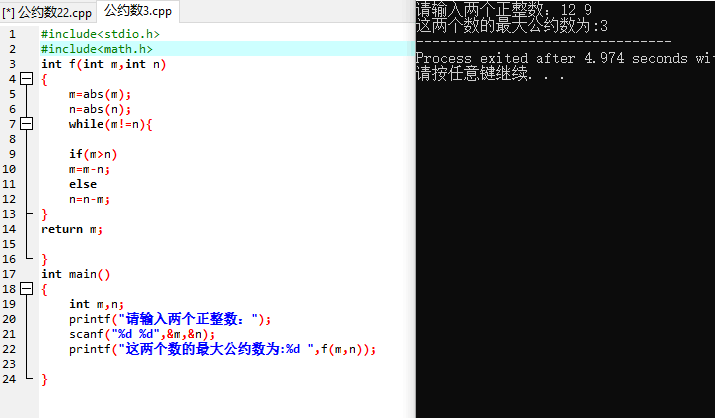
算法3：连续相减法

输入两个正整数a,b

如果a>b,a=a-b;

否则b=b-a;

直到a=b输出a或者b;

 

eg：a=12,b=9,a=12-9=3;

b>a,b=b-a=9-3=6;

b=b-a=6-3=3;

b=a,跳出循环，所以a或b为最大公因数。

#include<stdio.h>
#include<math.h> 
int f(int m,int n)
{
    m=abs(m);    //abs绝对值函数，需要导入<math.h>包 
    n=abs(n);    //用绝对值防止万一出现负数的情况 
    while(m!=n){
    if(m>n)
    m=m-n;
    else 
    n=n-m;
}
return m;

}
int main()
{
    int m,n;
    printf("请输入两个正整数："); 
    scanf("%d %d",&m,&n);
    printf("这两个数的最大公约数为:%d ",f(m,n));
     
}