2019-04-18 20:51:20
设a,b,c是三个塔座。开始时,在a塔座上一叠共有n个圆盘,这些圆盘自上而下,由大到小地叠在一起。各圆盘有小到大的编号为1,2,......,n,现要求将塔座a上的这一叠圆盘移到塔座b上,并仍按照同样顺序重叠。在移动圆盘时应遵守以下移动规则。
1.每次只能移动一个圆盘。
2.任何时刻都不允许较大的圆盘压在较小的圆盘之上。
3.在满足1和2的条件下,可将圆盘移到a,b,c的任一座塔座上。
递归解法:
移动圆盘的方法:move(n,t1,t2,t3);将n个圆盘从t1移到t2,t3辅助。
1.将n-1个圆盘从t1移到t3:move(n-1,t1,t3,t2);
2.将最大的圆盘从t1移到t2;
3.将n-1个圆盘从t3移到t2;
算法设计(递归算法的例题)
void hanoi(int n,char a,char b,char c){ if(n==1) { printf("move disk %d from %c to %c ",n,a,b); } else { hanoi(n-1,a,c,b); //将n-1个盘子从a移动到c printf("move disk %d from %c to %c ",n,a,b); hanoi(n-1,c,b,a); //将n-1个盘子从c移动到b; } } /*字符常量a,b,c代表三个位置*/ int main(){ int n; char a,b,c; scanf("%d",&n); hanoi(n,'a','b','c'); }
当有3个汉诺塔和3个盘子时,结果为:
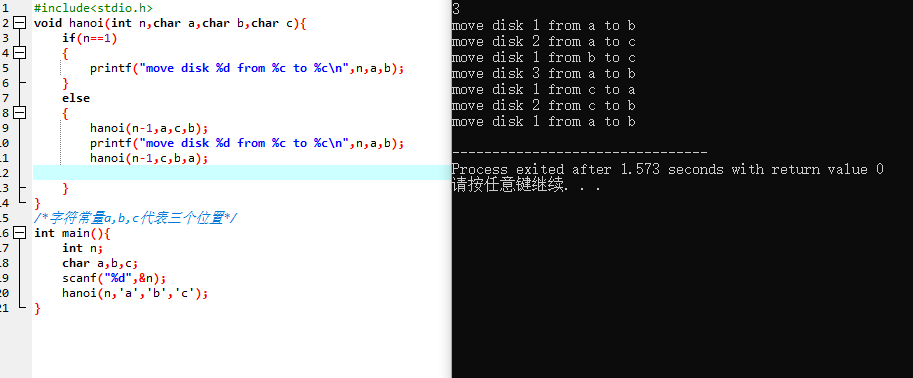
思考???
当有4个汉诺塔为:
void hanoi(int n,char a,char b,char c,char d){ if(n==1) { printf("move disk %d from %c to %c ",n,a,b); } else { hanoi(n-1,a,c,d,b); printf("move disk %d from %c to %c ",n,a,b); hanoi(n-1,c,b,d,a); } } /*字符常量a,b,c代表三个位置*/ int main(){ int n; char a,b,c,d; scanf("%d",&n); hanoi(n,'a','b','c','d'); }
先进行4个汉诺塔3个盘子时的算法设计,1号盘子移到d,2号盘子移到c,1号移到c,再把3号盘子移到b,1号移到b,2号移到b.
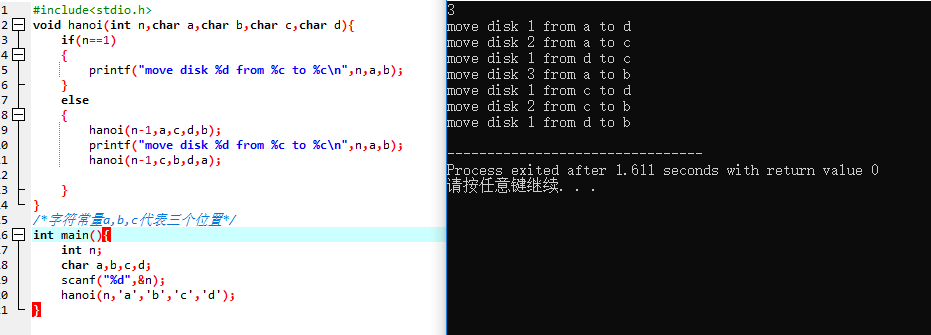
当有4个盘子时,同样采用递归方法
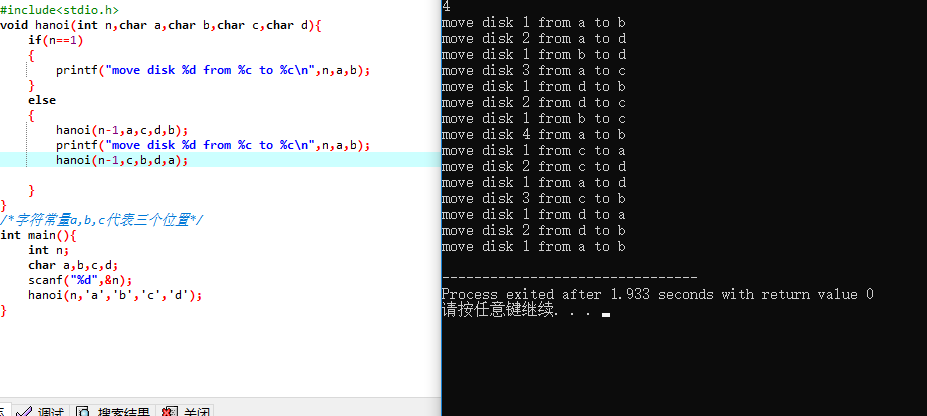
终于解决了心心念念的汉诺塔问题!!!