爱丽丝在亚的斯亚贝巴(埃塞俄比亚首都),过了新年之后,得意地说:除了某个半球之外,她过新年的地方包括地球上任意一个可能的半球。那么,爱丽丝至少去过几个地方过新年?
注:我们将爱丽丝去过的地方视为地球上的一个点。半球的边界不包括在半球内。
本题答案是4。
 左图为地球。
左图为地球。
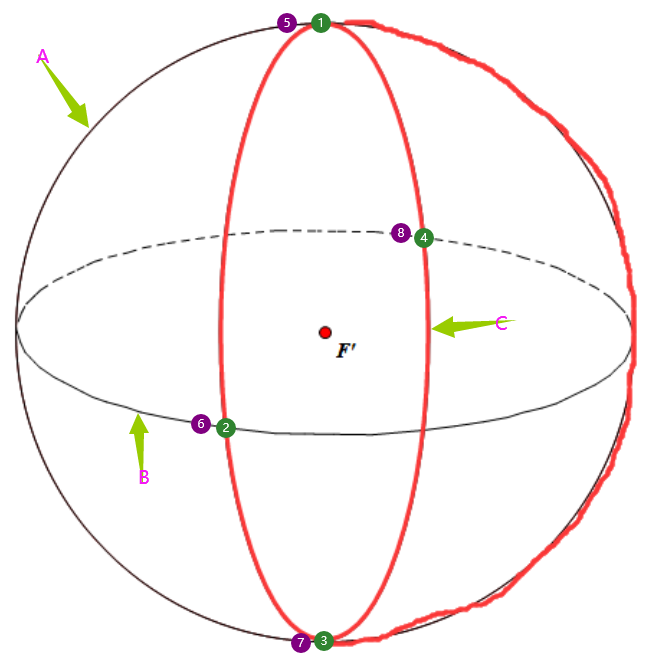
假设红色半球是爱丽丝未到过的半球,该半球上任一点爱丽丝都没去过。1、3是圆A、C的交点,2、4是圆B、C的交点。 5是圆A上无限接近1的点,6是圆B上无限接近2的点,7是圆A上无限接近3的点,8是圆B上无限接近4的点。5 6 7 8都不在红色半球上。
由于除了红色半球之外,她过新年的地方包括地球上任意一个可能的半球。将红色半球绕圆C平行纸面逆时针旋转无限小的度数得到一个新的半球,那么爱丽丝肯定到过这个半球,所以爱丽丝肯定到过点5;再把红色半球绕圆C平行纸面顺时针旋转无限小的度数,绕圆C垂直纸面顺时针旋转无限小的度数、逆时针旋转无限小的度数,可分别得出爱丽丝到过点7、6、8。所以爱丽丝至少去过四个点(点5 6 7 8)。下面证明只要爱丽丝去了5 6 7 8四个点就能满足题意。
假设只去点5 6 7 8不能满足题意,即除了红色半球外,至少存在一个爱丽丝没去过的半球。将红色半球的互补半球命名为Q,再令半球F为除了红色半球外,爱丽丝没去过的半球,那么F上肯定不包括点5 6 7 8,令半球Y是F的互补半球,那么Y上肯定同时包括点5 6 7 8。由于F≠红色半球,所以Y≠Q。经分析易知,Y与圆B有两个交点,将这两个交点命名为点9、10,同时Y与圆C也必然有两个交点,将其命名为点11、12,易知点9、10 点11、12所在的直线经过球心F‘。由于Y上有点6 8,又因为点6、8无限接近于点2、4,所以点9、10构成的直线必然与点2 4构成的直线重合(因为如果不重合的话,点6 8就会在点9、10构成的直线两侧了,那么半球Y上必然不会同时有点6和点8),又因为点9 10 2 4都在圆B上,所以点9 10必然与点2 4重合,同理点11、12必然与点1 3 重合。又因为点9 10 11 12都在Y上,所以点 1 2 3 4也在Y上,所以半球Y是红色半球或是半球Q。因为F是爱丽丝没去过的半球,所以F≠Q,所以Y≠红色半球,又因为之前得到了Y≠Q,所以推出矛盾,假设不成立,即:去了5 6 7 8点之后除了红色半球外不存在其他爱丽丝没去过的半球。所以爱丽丝至少得去4个地方过新年。