一道计数题 出题人：中国科学技术大学 苏淳

在白色6*6方格表中染红一些方格，使得每行每列都恰好有两个红格，求不同的染法数目。

如果染色方案A得到的方格表可以通过交换行或列得到染色方案B，则称AB方案是等价的。

经分析可知，一共有三种”基本的染色方案“，这三种染色方案互不等价，并且所有的染色方案都可通过这三种基本方案交换行或列得到。

基本方案如下：

1.  2. 3.

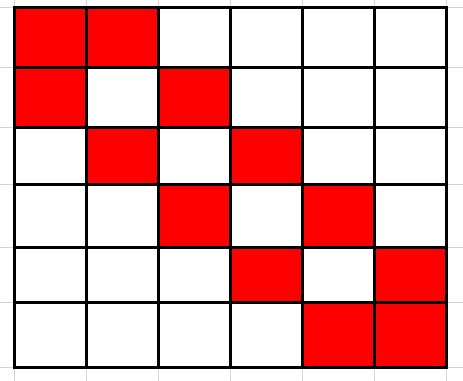
这三个方案等价的染色方案数目之和就是总的染色方案数目。

根据每个方案的特征，利用排列组合知识可得：

N₁=C₆²*5*C₄²*3，N₂=C₆²*C₆²*C₄²*3*2*2，N₃=C₆²*5*4*4*(C₃²*2+C₃¹*3*2*2)，

所以总的染色方案数 N=N₁+N₂+N₃