已知n是正整数,把n*n的正方形分成n方个单位正方形,将111枚硬币放入这些单位正方形中使得任意两个相邻(有一条公共边)的单位正方形中数量之差的绝对值恰好为1 ( 单位正方形内可以没硬币) ,求n的最大值。
·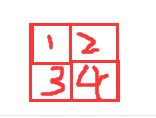
考虑一个2*2的正方形,因为2 3都与1相差1或-1,所以2 3硬币之和为偶数,同理1 4硬币之和为偶数,所以一个2*2的硬币数为偶数。而因为任意N*n(n为偶数)的正方形都可以分割为若干个2*2的正方形,所以N*n(n为偶数)的正方形的硬币数为偶数。所以对于本题,n必为奇数,所以只考虑奇数即可。
对于一个2*2的小正方形来说,其硬币数最少为2。因为1 2 3 4里至多有两个为0。所以一个以N*n(n为偶数)的正方形内的硬币数至少为n*n/2。而16*16/2=128>111,所以n<17。
考虑一下15*15.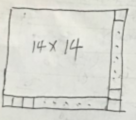 把其划分为两部分,一部分为14 14的,另一部分为剩下的。对于14 14这部分,这部分的硬币数最少为98个。对于剩下的部分,因为相邻两个的硬币数不能相同,所以这部分的硬币数最少14个(0 1相隔放置,角落放0个),所以15*15的硬币数最少为112个。所以n<=13。
把其划分为两部分,一部分为14 14的,另一部分为剩下的。对于14 14这部分,这部分的硬币数最少为98个。对于剩下的部分,因为相邻两个的硬币数不能相同,所以这部分的硬币数最少14个(0 1相隔放置,角落放0个),所以15*15的硬币数最少为112个。所以n<=13。
对于13*13的来说  ,先用这种方式放硬币,可知一共在85个单位正方形放了85个硬币,每个正方形内放一个,还剩下84个空的正方形,此时再把26个硬币分成13份,每份两个,随便找13个0放进去。由于0+2=2 2-1=1,85+26=111,且所有的0的都被1包围。所以满足题意。
,先用这种方式放硬币,可知一共在85个单位正方形放了85个硬币,每个正方形内放一个,还剩下84个空的正方形,此时再把26个硬币分成13份,每份两个,随便找13个0放进去。由于0+2=2 2-1=1,85+26=111,且所有的0的都被1包围。所以满足题意。
综上,n最大为13。