平面上给定25个点，已知其中任何三点中总有两点的距离小于1，证明：可以画一个半径为1的圆覆盖其中至少13个点。
证明：本题也非常简单。首先考虑：其中任何三点中，三个点的距离都小于1
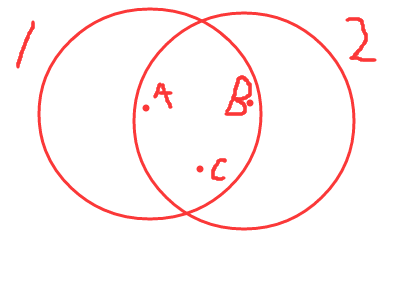从中任选三点ABC，1 2分别是以A B为圆心半径=1的圆，易知ABC都在1 2圆的重叠部分。考虑其他22个点与AB 两点的组合。易知其他22个点也都在1 2圆的重叠部分。
再考虑至少有两点距离>=1的情况
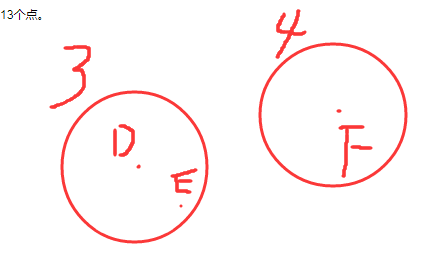DF是距离大于1的两点，DE距离小于1，3 4分别是以D F为圆心半径=1的圆。考虑其他22个点与DF 两点的组合。易知其他22个点也都在3圆或4圆内。当其中有>=12个点在4圆内时，4圆内的点就>=13个；当其中有<12个点在4圆内时，3圆内的点就>=13个。
综上：存在一个半径为1的圆覆盖其中至少13个点。