
先讨论 n<m。
首先明白一个事实:正方形周长之和=2m+2n+2*矩形内线段长度。正方形边长之和=正方形周长 / 4。因为矩形内部的线段的两侧肯定是两个正方形,所以计算周长时要算两次。
本解答是先求得矩形内线段长度min,然后得到边长之和的min的。
另一个事实:如果矩形内部最大的正方形的边长小于n,那么矩形内线段长度肯定>=m+n。这个结论很显然,因为如果最大的正方形的边长小于n,矩形内任意一条平行于n的线都会与线段相交,这是因为矩形被正方形所填充没有空白,所以水平的线段长度肯定大于等于m。同理竖直的线段长度肯定大于等于n,所以:如果矩形内部最大的正方形的边长小于n,那么矩形内线段长度肯定>=m+n。
另一个事实:对于矩形内部最大的正方形的边长等于n的情况。任何一种边长=n的正方形不紧贴AD/CB边的策略的周长和>=边长为n的正方形紧贴AD/CB边的策略的周长和的最小值。
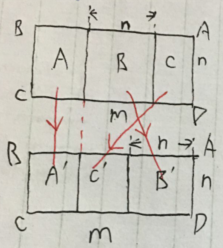 可以用反证法证明。假设存在一种边长=n的正方形不紧贴AD边的策略的周长和<边长为n的正方形紧贴AD/CB边的策略的周长和的最小值。不妨令左图的上图为不紧贴AD/CB边的周长和最小的策略。其中B是边长为n的正方形,两侧为A C区域, 两区域不存在紧贴AD/CB边的边长为n的正方形。现在我们做一下平移变换,把B平移到紧贴AD处,C区域整体移到B‘左侧,A区域不动。此时得到的这种填充方法的正方形的周长和显然与上图相等。而下图策略的周长和>=边长为n的正方形紧贴AD/CB边的策略的周长和的最小值。推出矛盾,假设不成立,所以:任何一种边长=n的正方形不紧贴AD/CB边的策略的周长和>=边长为n的正方形紧贴AD/CB边的策略的周长和的最小值。
可以用反证法证明。假设存在一种边长=n的正方形不紧贴AD边的策略的周长和<边长为n的正方形紧贴AD/CB边的策略的周长和的最小值。不妨令左图的上图为不紧贴AD/CB边的周长和最小的策略。其中B是边长为n的正方形,两侧为A C区域, 两区域不存在紧贴AD/CB边的边长为n的正方形。现在我们做一下平移变换,把B平移到紧贴AD处,C区域整体移到B‘左侧,A区域不动。此时得到的这种填充方法的正方形的周长和显然与上图相等。而下图策略的周长和>=边长为n的正方形紧贴AD/CB边的策略的周长和的最小值。推出矛盾,假设不成立,所以:任何一种边长=n的正方形不紧贴AD/CB边的策略的周长和>=边长为n的正方形紧贴AD/CB边的策略的周长和的最小值。
下面考虑一种特殊的策略:
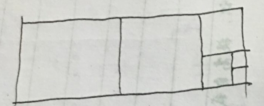
这种策略是贴着短边放与边长与短边相等的正方形,放不下了再在剩下的那个小矩形里贴着小矩形的短边放与边长与小矩形短边相等的正方形···
下面证明这种策略肯定能使正方形填充满整个矩形:
利用反证法,假设最后没有使正方形填充满整个矩形,那么肯定最后剩了个矩形,因为如果最后剩了个正方形那么就满足题意了。不妨设最后剩下的矩形为a*b,如果a、b有一个为1,那么显然这个矩形可以分割为边长为1的正方形。如果a、b均不为1,不妨让a<b,那么我们可以贴着a边继续放边长为a的正方形,也就是说可以继续填充,与该矩形是最后剩下的矩形这一假设矛盾,所以这种方法可以使正方形填充满整个矩形。
下面再讨论这种方法填充的最小的正方形的边长与m n之间的关系。
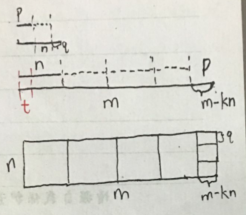
不妨以上图为例进行一下分析:令t为m n的最大公约数。先贴着左侧短边放边长为n的正方形,放到放不下为止。直到剩了一个m-kn*n的矩形,令p=m-kn。下面证明一下n与p的最大公约数也是t:
不妨设n=c*t,m=d*t。其中c、d为正整数。p=m-kn=d*t-c*k*t=(d-c*k)t。所以t也是p的约数。接着用反证法证明n与p的最大公约数也是t:
假设n与p的最大公约数大于t,不妨设其为x且n/x=e,p/x=f, 所以m=p+kn=fx+ekx=(ek+f)x。所以x也是m n的公约数,而x>t,与t是m n的最大公约数矛盾,所以假设不成立,所以n与p的最大公约数不大于t。而又因为t是p n的公约数,所以n与p的最大公约数也是t。
继续沿着p边切割,切到放不下为止,剩下的小矩形的短边为q,同理可得p q的最大公因数也为t,继续向下切割·······

假设最后的分割图是上图,右下角的图是上图右下角的局部放大图。在上图中的红丨 是切割的最后一步。切割完成后,整个矩形被切割成若干个正方形。很显然ACHD 、BCHE是最后得到的正方形,也是最小的正方形,最后得到的正方形在整个大矩形的右下角与我们的切割方法有关,如果一直贴着左边和上边切,最后的正方形就在右下角,值得一提的是,切割时选择从哪条边对最后的结果没有任何影响。 对于右下角这个局部放大图,根据之前的类比推理可知,AF AB AD的最大公约数为t。又因为AB和AD的最大公约数为AD(因为ABED可以被均分为几个边长为AD的正方形),所以AD=t,而AD是最小的正方形的边长,所以整个切割完的矩形里的最小的正方形的边长就是t。
下面求一下矩形内的线段的长度:
矩形内的线段的长度就是其对应的正方形的边长。我们设a1 a2 ···· ax分别为边长最大、边长第二大·····边长最小的正方形的边长,b1 b2 ···· bx为其对应的线段总长。
通过简单的几何知识可知,bx=ax-1 - ax ; bx-1 = ax-2 - ax ; bx-2 = ax-3 - ax-1 ; bx-3= ax-4 - ax-2 ; bx-4 = ax-5 - ax-3 ····· b3=a2 - a4 ; b2 = a1 - a3 ; b1= m - a2
该策略下的矩形内的线段的总长度 L = b1 + b2 + ···· bx-1 + bx = m + a1 - 2ax = m + n - 2(m , n) (m , n)是m n的最大公因数。
下面证明该策略下矩形内的线段的总长度就是可能得到的最小的线段总长度:
之前证明了:如果矩形内部最大的正方形的边长小于n,那么矩形内线段长度肯定>=m+n。而该策略下的线段长度= m + n - 2(m , n)<m+n。所以当矩形内部最大的正方形的边长小于n时,矩形内线段长度肯定大于该策略。又因为边长=n的正方形不紧贴AD/CB边的策略的周长和>=边长为n的正方形紧贴AD/CB边的策略的周长和的最小值,所以最小的线段长度肯定在紧贴短边放边长与短边相等的正方形时取得。 因为该策略就是一直紧贴短边放边长与短边相等的正方形直到放不下为止,所以该策略得到的线段长度就是可以得到的最短的线段总长。
所以正方形周长之和的最小值=2m+2n+2*(m + n - 2(m , n) )=4m+4n-4(m , n) 。正方形边长之和的最小值=正方形周长之和的最小值 / 4 = m + n -(m , n)
上述讨论的是n<m的情况, 当n=m时,显然正方形边长之和的最小值=n =m + n -(m , n)
所以最终答案:正方形边长之和的最小值 = m + n -(m , n)