在下面的内容中,我们用C来表示需要分的类数。
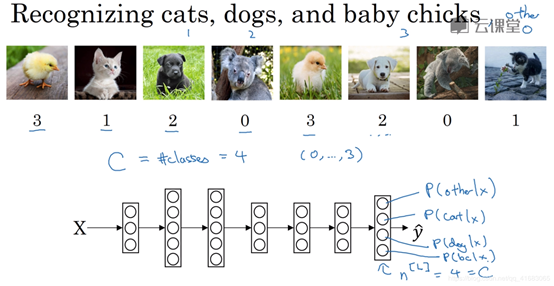
最后一层的隐藏单元个数为4,为所分的类的数目,输出的值表示属于每个类的概率。
Softmax函数的具体步骤如下图:

简单来说有三步:
计算z值(4×1矩阵)
将z作为指数,得到中间变量t(维度同z)
对t归一化,得到a(维度同t,同z)。
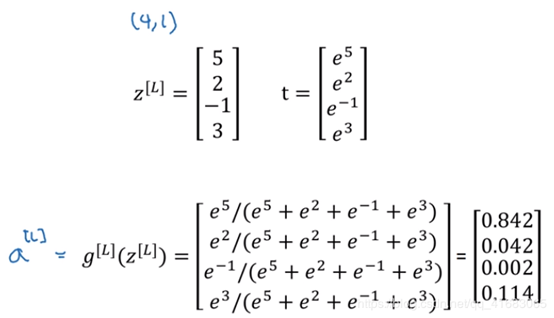
Softmax激活函数的特殊之处在于,输入一个向量,最后输出一个向量。
Softmax的示例
下面我们来来考虑一个只有输出层没有隐藏层的神经网络。
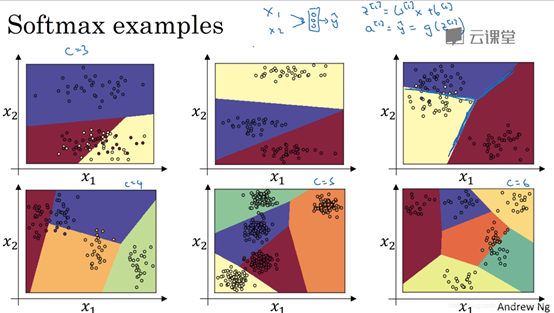
在这张图表中,我们所做的是选择图中的数据作为训练集,用数据的C种标签来训练Softmax分类器。图中的颜色显示了Softmax分类器的输出的阈值(输入的着色是基于三种输出中概率最高的那个)。
由此我们可以看出,Softmax回归是logistic回归的一般形式,有类似线性的决策边界,但有超过两个分类。
需要注意的是,以上所有的线都是线性决策边界,将数据分到C个类中。
Softmax的损失函数
损失函数的定义:

y是预期结果 y冒是实际结果
分割线下面的是向量化的实现,Y是所有样本的预期结果的集合,维度是(4,m)m是样本数,4是指的最后的输出结果向量是4维的。Y帽是所有样本的实际计算结果的集合。
梯度下降的实现
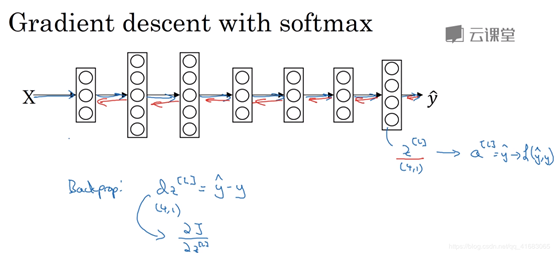
J对z[l]的梯度是y帽-y。z[l]的含义在上面,往上翻一下就能看见。是将z[l]代入到softmax分类器得到概率结果的。
但现有的深度学习框架不需要我们计算梯度了,只要我们完成正向传播,系统会自动实现反向传播。