正则化网络激活函数（Batch归一化）：
在神经网络训练中，只是对输入层数据进行归一化处理，却没有在中间层进行归一化处理。要知道，虽然我们对输入数据进行了归一化处理，但是输入数据经过σ(WX+b)σ(WX+b)σ(WX+b)这样的矩阵乘法以及非线性运算之后，其数据分布很可能被改变，而随着深度网络的多层运算之后，数据分布的变化将越来越大。如果我们能在网络的中间也进行归一化处理，是否对网络的训练起到改进作用呢？答案是肯定的。
这种在神经网络中间层也进行归一化处理，使训练效果更好的方法，就是批归一化Batch Normalization（BN）。BN在神经网络训练中会有以下一些作用：
- 加快训练速度
- 可以省去dropout，L1, L2等正则化处理方法
- 提高模型训练精度
- 三、BN的原理
BN可以作为神经网络的一层，放在激活函数（如Relu）之前。BN的算法流程如下图：
1.求每一个小批量训练数据的均值
2.求每一个小批量训练数据的方差
3.使用求得的均值和方差对该批次的训练数据做归一化，获得0-1分布。其中ε是为了避免除数为0时所使用的微小正数。
4.尺度变换和偏移：将xi乘以γ调整数值大小，再加上β增加偏移后得到yi，这里的γ是尺度因子，β是平移子。
这一步是BN的精髓，由于归一化后的xi基本会被限制在正态分布下，使得网络的表达能力下降。为解决该问题，我们引入两个新的参数：γ,β,y。 γ和β是在训练时网络自己学习得到的。
将Batch-Norm 拟合进神经网络的方法
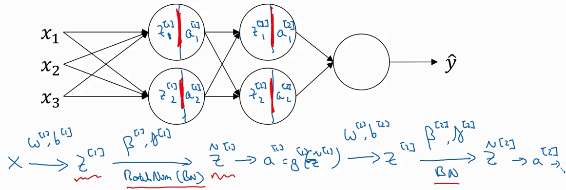
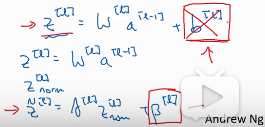
BN应用在Z→a之间。可以认为BN是在z a之间加的一层隐藏层。在BN中，Z的计算式没有b这一项，即Z=Wa ≠wa+b
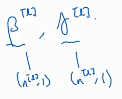贝塔、伽马的维数都是（n[l] ,1） n[l]是第l层的隐藏单元数，也就是说每个隐藏单元都有对应的贝塔、伽马。由于BN可看做是在z a之间加的一层隐藏层，所以求
就和
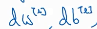有着一样的意义。所以也应对贝塔、伽马应用梯度下降法更新其值。
这个是最基本的梯度下降法，还可以对贝塔、伽马应用最近提到的动量梯度下降、ADAM方法等更新贝塔、伽马参数。
mini-bitch会把训练集分为很多份，每份都会求得一个u、σ，那么对于预测集来说，应该怎么取u、σ呢？
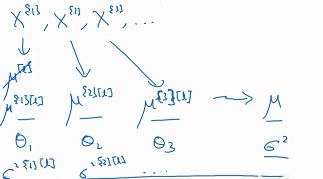这就是计算u的方法，用到了指数加权平均法，θ0=0，θ1=（1-β）θ0+βu[1][l]，θ2=（1-β）θ1+βu[2][l]。最后的θ就是我们要用到预测集的u。u[i][l]是第i个mini-bitch第L层的u平均值。计算σ2的方法与之相同。
再说一下训练集、测试集、验证集的区别。训练集的工作过程：首先给定超参数。然后系统初始化，随机设置W b 等参数，然后进行正向传播得到最终结果，然后再将得到的结果与预期结果进行对比，如果误差在允许范围内，那么就结束训练，如果误差大，那么就进行反向传播，计算J对各参数的梯度，然后将参数进行更新，更新后再进行正向传播，得到新的结果，再看这个结果是否达到预期，达到预期就结束，没达到预期就再反向传播······ 需要注意的是训练集不会对超参数进行选择，超参数是事先我们定好的。训练集最后得到的是J满足预期的情况下的W b等一般参数。测试集：测试集的作用是选择合适的超参数。 由于训练集无法对超参数进行选择，所以我们就设置不同的超参数在训练集训练，然后得到其对应的w b一般参数。再把不同超参数对应的神经网络代入到测试集进行测试，看看哪个超参数对应的准确率高。 验证集：把在测试集表现最好的超参数及其神经网络代入到验证集，得到最后的准确率。
训练集有正向传播和反向传播。 测试集和训练集只有正向传播没有反向传播。