超参数
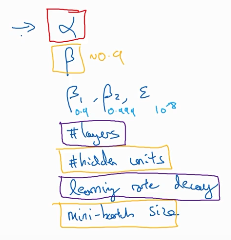
主要的超参数是上面几个，最重要的是红色的 学习率，其次是黄色的 m-b尺寸、隐藏层层数、动量梯度下降的贝塔。
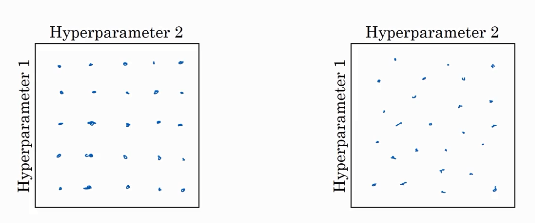
左图是早期超参数选择的方法：以两个超参数的选择为例，在网格中均匀布置一些点，然后将这些点全部试一遍，哪个效果好用哪个。右图是之后有的随机选择点的方法，把随机选择的点全部试一遍，哪个好用哪个。这个是二维参数（两个参数）的情况，三个参数就要立体的了，更多参数就是更高维。
另一个惯例是采用由粗糙到精细的策略，也许你会发现效果最好的某个点，这个点周围的其他一些点效果也很好。之后放大这块小区域，然后在其中更密集地取值，找更佳的参数点。
为超参数选择合适的范围：
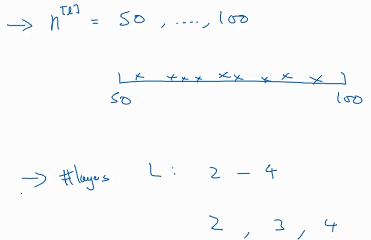如果我们猜测隐藏层的单元数的最佳值在50-100之间，神经网络层数的最优值在2-4之间，我们想找到这个最佳值，那么就要在这个区间中列出一些点，看看哪个效果更好，此时 取值方法用均匀取值较为合理。
但是如果想找到学习率0.0001到1之间的最佳值，用均匀取值就不合适了。可以用对数取值，下面两个式子是在0.0001-1之间对数取值的方法。右图是更一般的方法，a是以10为底左端点的对数。b是以10为底右端点的对数，r在a、b之间均匀取值，埃尔法=10的r次方。
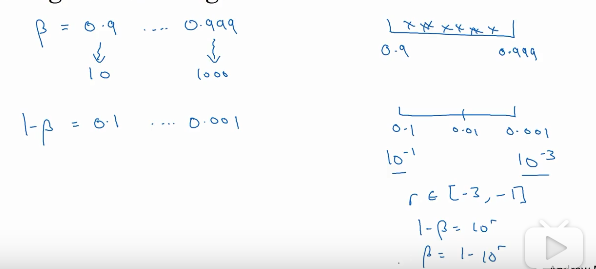
另一个例子是对随机加权指数贝塔的取值，如果贝塔想在0.9-0.999之间取值，好的方法是先对1-贝塔取值，再用1-it。因为1-贝塔=0.1-0.001，所以就可以用之前的方法了。 右下角的三个式子就是取值方法。