线性神经网络

介绍

线性神经网络在结构上和感知器网络非常相似，只是神经元传输函数不同。

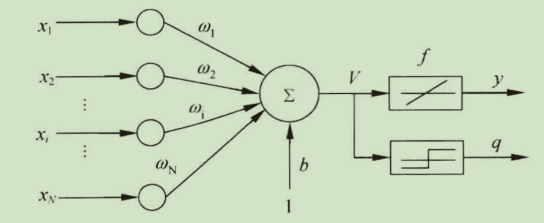
假设输入向量为：

 

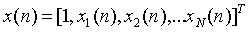
权值向量为：

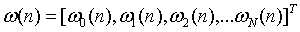
则输出可以表示为：

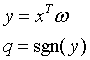
 LMS学习算法

线性什么网络学习的目标是找到适当的w，使得误差的均方差mse最小，在实际计算中，为了解决权值w的维数过高，计算较复杂的问题，采用梯度下降法，从空间某一点开始，沿着负梯度方向，最终达到最小值。

误差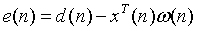

代价函数：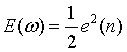

权值调整规则：

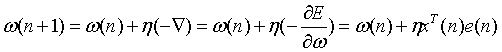
收敛条件的选择

收敛条件的选择对算法有较大的影响，常用的条件有：

• 误差等于0或者小于事先规定的值。
• 权值变化量已经很小，
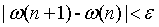
• 设置最大迭代次数，达到最大迭代次数后，算法强制结束

学习率的选择

学习率过小，则算法耗时过长；学习率过大，则可能导致误差在某个水平上反复振荡，影响收敛的稳定性。

1996年Hayjin证明，只要学习率满足下式，LMS算法就是按方差收敛的：

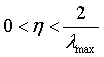
其中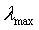是输入向量x(n)组成的自相关矩阵R的最大特征值，由于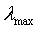常数通常不可知，因此往往是由自相关矩阵R的迹来代替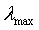。自相关矩阵主对角线元素就是个输入向量的均方值。因此公式又可以写 成：

 学习率随着学习的进行逐渐下降比始终不变更加合理。在学习初期，使用较大的学习率保证收敛速度，随着迭代的增加，减小学习率保证精度，确保收敛。

线性神经网络和感知器对比

感知器和线性神经网络在结构上非常相似，唯一的区别在于传输函数，感知器传输函数为一个简单的二值阈值元件；线性神经网络的传输函数是线性的。这就决定了感知器只能做简单的分类，而线性神经网络可以实现拟合或者逼近。

LMS学习算法得到的分类边界往往处于两种模式的正中间，而感知器学习算法在刚刚能正确分类的位置就停下来了，从而使分类边界离一些模式较近，使系统对误差较为敏感。

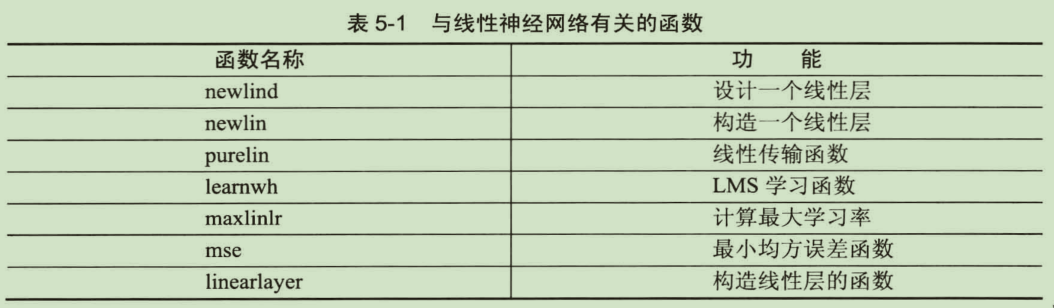
线性神经网络相关函数

x=-5:5;
y=3*x-7;
randn('state',2);
y=y+randn(1,length(y))*1.5;
plot(x,y,'o')
P=x
T=y
net=newlind(P,T);  %返回已经训练好的线性神经网络
new_x=-5:0.2:5;
new_y=sim(net,new_x);  %仿真测试
hold on
plot(new_x,new_y)
net.iw   %[2.9219]
net.b    %[-6.6797]