SLAM基础

SLAM(Simultaneous Location and Mapping,同时定位与地图构建），它是指搭载特定传感器的主体，在没有环境先验信息的情况下，于运动过程中建立环境的模型，同时估计自己的运动。

经典视觉SLAM框架

视觉里程计（Visual Odometry,VO)

估算相邻图像间相机的运动，以及局部地图的样子。由于VO只使用相邻2张图片估计相机运动，因此会产生累积漂移，为了解决漂移问题，需要使用后端优化和回环检测技术。VO称为前端，前端给后端提供待优化的数据，以及这些数据的初始值，后端负责整体的优化过程。

后端优化（Optimization)

接受不同时刻视觉里程计测量的相机位姿，以及回环检测的信息，对它们进行优化，得到全局一致的轨迹和地图。

回环检测（Loop Closing)

判断机器人是否曾经到达过先前的位置。为了实现回环检测，我们需要让机器人具有识别曾经到达过的场景的能力。可以通过判断图像间的相似性，来完成回环检测。在检测到回环之后，我们会把“A 与 B 是同一个点”这样的信息告诉后端优化算法。然后，后端根据这些新的信息，把轨迹和地图调整到符合回环检测结果的样子。这样，如果我们有充分而且正确的回环检测，就可以消除累积误差，得到全局一致的轨迹和地图。

建图（Mapping)

根据估计的轨迹，建立与任务要求对应的地图。大体上讲，可以分为度量地图和拓扑地图两种。

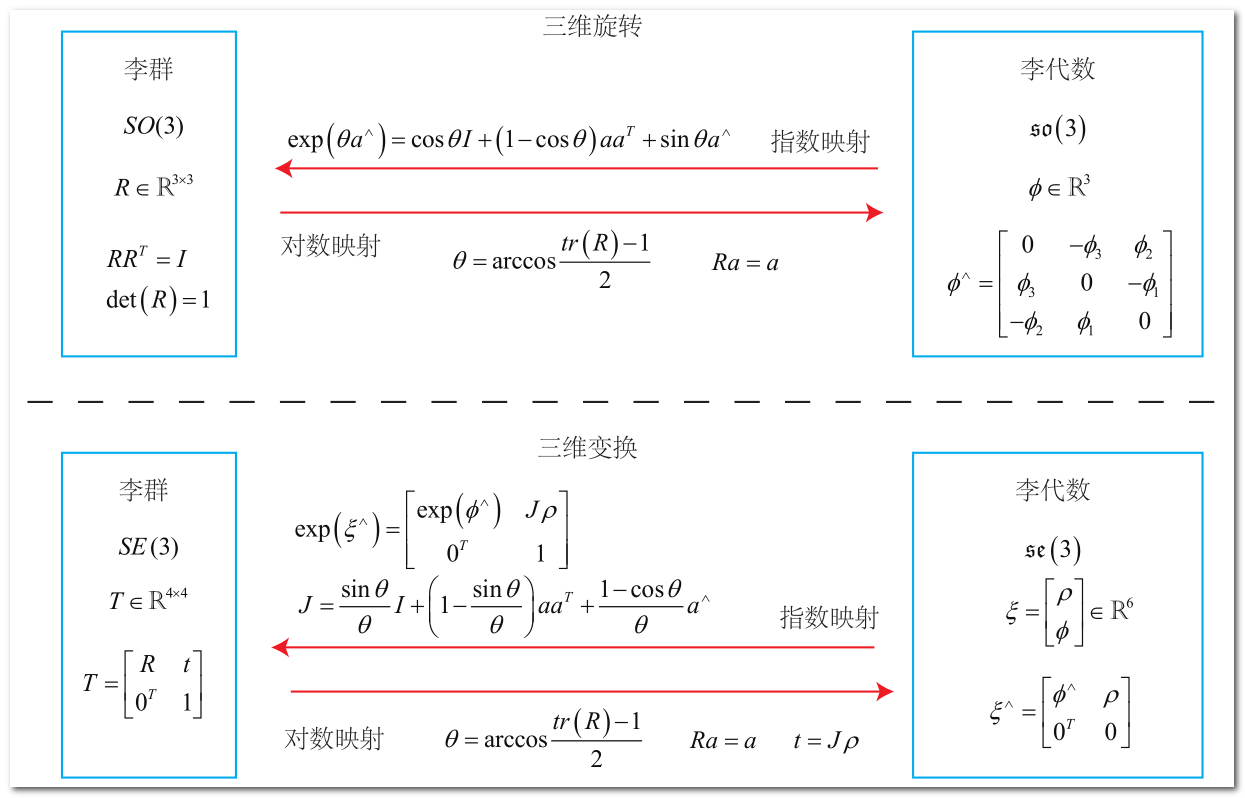
 特殊正交群SO(n) Special Orthogonal Group

  

SO(3)就表示三维空间中的旋转。

特殊欧氏群SE(3)

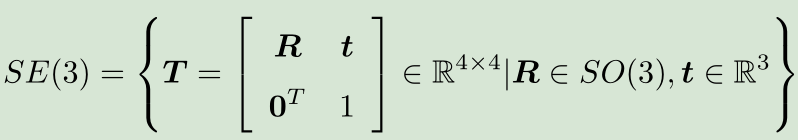
SLAM问题的数学描述

 

三维旋转的表示

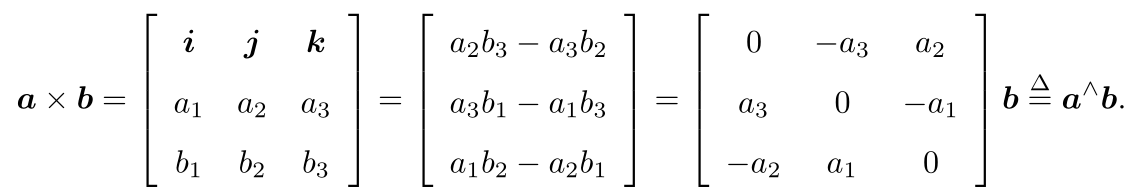
两个向量的外积等于第一个向量的反对称矩阵与第二个向量的乘积。

理论上可以证明，只要我们想用三个实数来表达三维旋转时，都会不可避免地存在奇异性问题。

•  旋转矩阵，用九个量描述三自由度的旋转，具有冗余性。
• 轴角表示，通过罗德里格斯公式（Rodrigues’s Formula ）实现和旋转矩阵之间的相互转换。
• 欧拉角，使用三个分离的转角，把一个旋转分解成三次绕不同轴的旋转。当然，由于分解方式有许多种，所以欧拉角也存在着不同的定义方法。比如说，当我先绕 X 轴旋转，再绕 Y 轴，最后绕 Z 轴，就得到了一个 XY Z 轴的旋转。同理，可以定义 ZY Z、ZYX等等旋转方式。如果讨论更细一些，还需要区分每次旋转是绕固定轴旋转的，还是绕旋转之后的轴旋转的，这也会给出不一样的定义方式。存在万向锁（奇异性）问题。
• 四元数，既是紧凑的，也没有奇异性。我们能用单位四元数表示三维空间中任意一个旋转

四元数表示<-->轴角表示

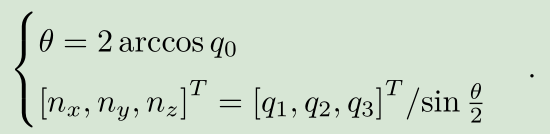
旋转矩阵表示-->四元数表示

 四元数表示旋转

#include <iostream>
using namespace std;

#include <Eigen/Core>
#include <Eigen/Geometry>
#define M_PI       3.14159265358979323846   // pi
/****************************
* 本程序演示了 Eigen 几何模块的使用方法
****************************/

int main(int argc, char** argv)
{
    // Eigen/Geometry 模块提供了各种旋转和平移的表示
    // 3D 旋转矩阵直接使用 Matrix3d 或 Matrix3f
    Eigen::Matrix3d rotation_matrix = Eigen::Matrix3d::Identity();
    // 旋转向量使用 AngleAxis, 它底层不直接是Matrix，但运算可以当作矩阵（因为重载了运算符）
    Eigen::AngleAxisd rotation_vector(M_PI / 4, Eigen::Vector3d(0, 0, 1));     //沿 Z 轴旋转 45 度
    cout.precision(3);
    cout << "rotation matrix =
" << rotation_vector.matrix() << endl;                //用matrix()转换成矩阵
                                                                                      // 也可以直接赋值
    rotation_matrix = rotation_vector.toRotationMatrix();
    // 用 AngleAxis 可以进行坐标变换
    Eigen::Vector3d v(1, 0, 0);
    Eigen::Vector3d v_rotated = rotation_vector * v;
    cout << "(1,0,0) after rotation = " << v_rotated.transpose() << endl;
    // 或者用旋转矩阵
    v_rotated = rotation_matrix * v;
    cout << "(1,0,0) after rotation = " << v_rotated.transpose() << endl;

    // 欧拉角: 可以将旋转矩阵直接转换成欧拉角
    Eigen::Vector3d euler_angles = rotation_matrix.eulerAngles(2, 1, 0); // ZYX顺序，即roll pitch yaw顺序
    cout << "yaw pitch roll = " << euler_angles.transpose() << endl;

    // 欧氏变换矩阵使用 Eigen::Isometry
    Eigen::Isometry3d T = Eigen::Isometry3d::Identity();                // 虽然称为3d，实质上是4＊4的矩阵
    T.rotate(rotation_vector);                                     // 按照rotation_vector进行旋转
    T.pretranslate(Eigen::Vector3d(1, 3, 4));                     // 把平移向量设成(1,3,4)
    cout << "Transform matrix = 
" << T.matrix() << endl;

    // 用变换矩阵进行坐标变换
    Eigen::Vector3d v_transformed = T*v;                              // 相当于R*v+t
    cout << "v tranformed = " << v_transformed.transpose() << endl;

    // 对于仿射和射影变换，使用 Eigen::Affine3d 和 Eigen::Projective3d 即可，略

    // 四元数
    // 可以直接把AngleAxis赋值给四元数，反之亦然
    Eigen::Quaterniond q = Eigen::Quaterniond(rotation_vector);
    cout << "quaternion = 
" << q.coeffs() << endl;   // 请注意coeffs的顺序是(x,y,z,w),w为实部，前三者为虚部
                                                       // 也可以把旋转矩阵赋给它
    q = Eigen::Quaterniond(rotation_matrix);
    cout << "quaternion = 
" << q.coeffs() << endl;
    // 使用四元数旋转一个向量，使用重载的乘法即可
    v_rotated = q*v; // 注意数学上是qvq^{-1}
    cout << "(1,0,0) after rotation = " << v_rotated.transpose() << endl;

    return 0;
}

李群李代数

SO(3)和SE(3)对加法不是封闭的，即对两个旋转矩阵相加，则结果不再是一个旋转矩阵。但关于乘法是封闭的。

李群是指具有连续（光滑）性质的群，像整数群Z那样离散的群不是李群。而 SO(n) 和 SE(n)，它们在实数空间上是连续的。我们能够直观地想象一个刚体能够连续地在空间中运动，所以它们都是李群。

SO(3)对应的李代数

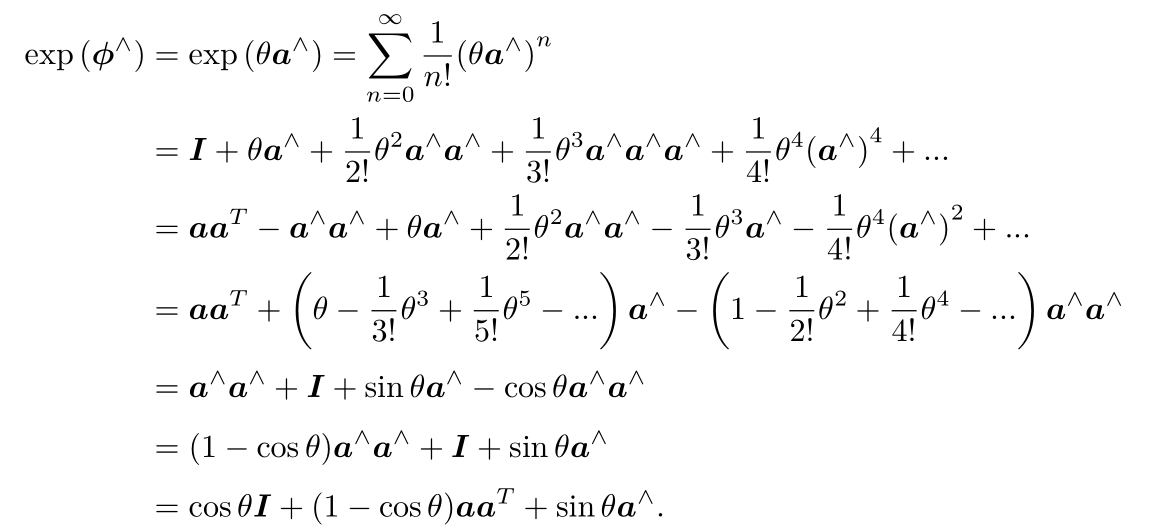
这表明，李代数so(3) 实际上就是由所谓的旋转向量组成的空间，而指数映射即罗德里格斯公式。

SE(3)对应的李代数

 

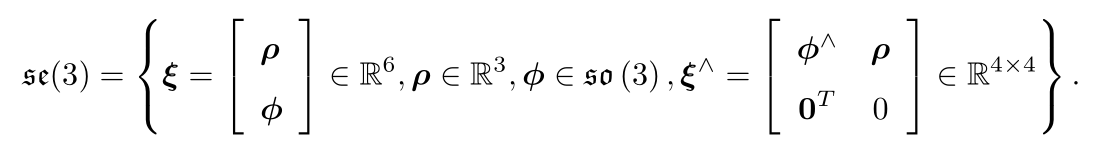
 指数映射：

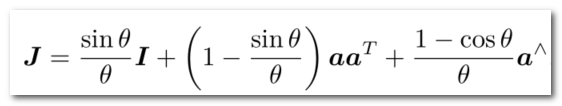
 平移部分经过指数映射，发生了一次以J为系数矩阵的线性变换。

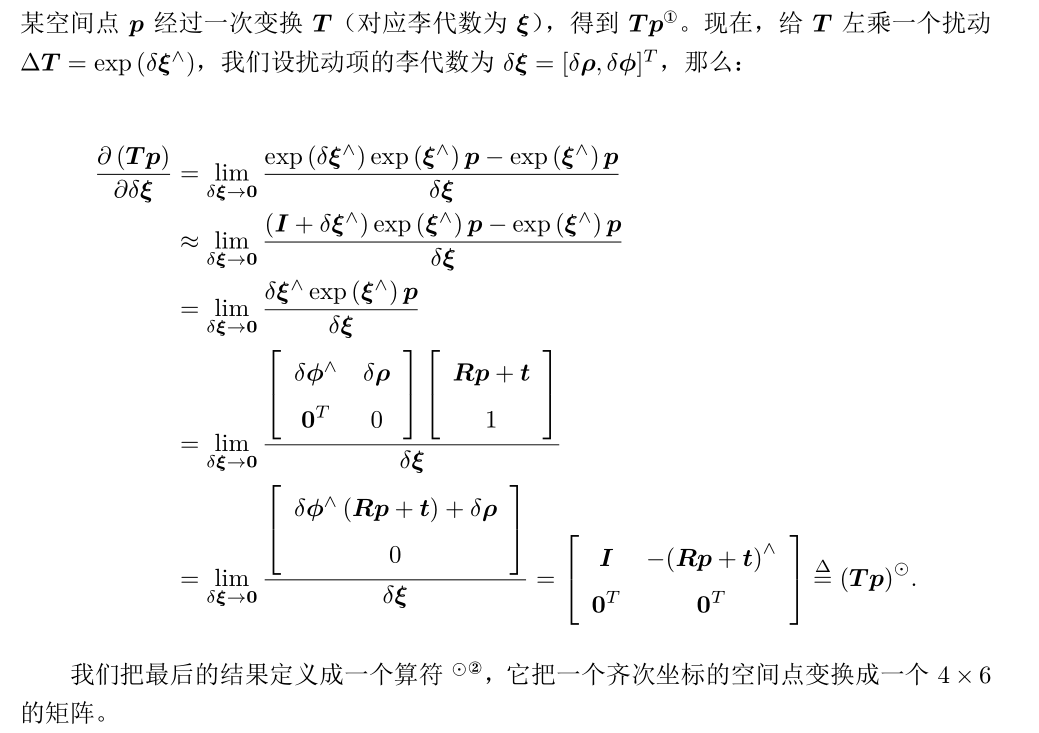
 SO(3)上的扰动模型

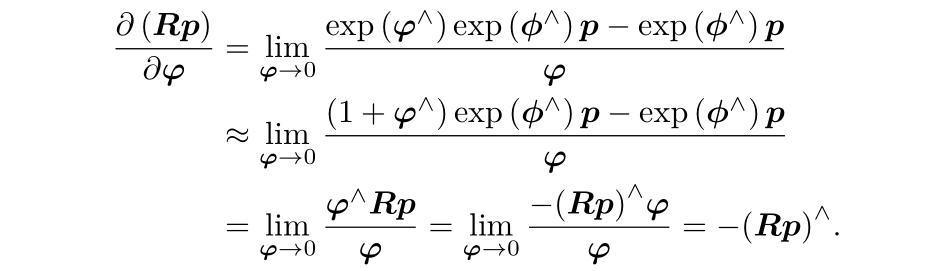
SE(3)上的扰动模型