首先我们要分清楚分类和回归的区别，分类问题是用于将事物打上一个标签，通常结果为离散值，回归问题通常是用来预测一个值，如预测房价、未来的天气情况等等。我们用申办银行信用卡的例子来进一步理解这两种问题的区别。
设想银行存有大量用户信息，比如年薪，年龄和居住地贷款等等，这些信息可以用在线性分类中，帮助银行确定能不能批准该用户的信用卡申请。但是除了确定能不能批准某个用户信用卡申请之外，银行还想给每个通过申请的用户设定一个信用卡限额。开始时是银行的工作人员通过用户信息确定用户信用卡限额，但是现在银行想借助工具自动实现这个任务，这就是一个回归问题。银行利用历史记录构建了一个数据集D （x1,y1), (x2,y2), ...,(xn,xn), xn是用户信息，yn是由银行工作人员根据用户信息设定的信用卡限额。 注意yn是一个实数（在这个例子中是正数），除了确定该用户能不能通过批准，银行还想要使用一个学习模型p代替工作人员来确定该用户的信用卡限额。银行希望用该模型预测出来的信用卡限额要近似人工计算出来的限额，这样的模型必然有很多，其中最简单最朴素的方法就是线性回归，也就是我们希望学习到一个线性模型。不过说是线性回归，学出来的不一定是一条直线，只有在变量x是一维的时候才是直线，高维的时候是超平面。
一 线性回归算法
线性回归算法的目标是最小化预测值与真实值之间的误差即让预测结果尽可能地拟合真实值。最常见的计算误差的形式是
在线性回归中，函数h将特征值与样本x进行线性组合
其中，b称为截距，或者bias， 为了方便我们定义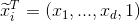
，i = 1,2,...,N, 
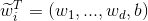, 即
，
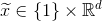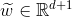将上边的等式写成下边的形式
在接下来的的公式中我们将忽略掉w和x上边的波浪号。
因此误差函数函数也就可以改写为
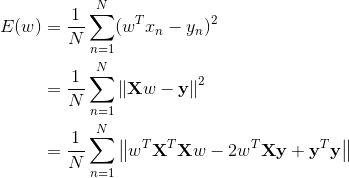
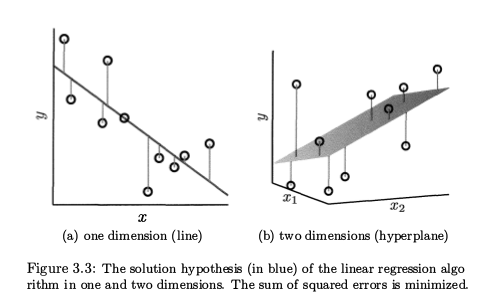
其中|| ||是向量的欧几里得范数，线性回归算法通过最小化损失函数计算出最优解。也就是求解出如下优化问题(argmin 或 argmax的意思是是求解函数的一组参数值，当使用这个参数时函数值达到最小（或最大）)：
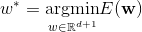
下面来直观理解一下线性回归优化的目标——真实值y就是在图中用圆圈表示出来，在(a)中预测值w^Tx_n就是y落在线段上的点，(b)中预测值w^Tx_n就是y落在平面上的点。(a)图中圆圈到他落在直线上的点距离就是预测值与真实值的误差的平方，损失函数就是这些距离和的平均值，通过最小化损失函数即最小化真实值到分割面的距离和来求解最优的w，最小化损失函数的方法有最小二乘法，梯度下降法等等。
如何求解就涉及到了凸函数的概念，可以看出线性回归的损失函数是凸函数，所以我们可以找到一个w的解使的损失函数值最小，通过凸函数的定义我们知道如果凸函数在c点处一阶导数(即梯度)为零 f'(c) = 0，则c是使f(x)取得最小值的点。所以我们可以通过求解
,来求出最优w，该损失函数的梯度是一个列向量，第i个元素为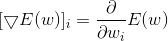
, 结合如下求导等式
(读者可以自行验证这两个求导等式)，我们对E(w) 中第三行的等式求导，得出E(w)的梯度
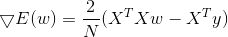
注意 w和E(w)的梯度都是列向量，当E(w)的梯度为0 时，w需满足
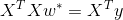
当X^TX的逆矩阵存在时，w有唯一解
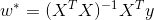
将其带入到预测函数中
接下来看一下我们寻找到的预测值的一个几何解释：从上面的解析解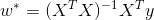
以及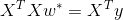
我们可以得到
（垂直的向量相乘=0），因此实际上ŷ 是y在平面X（由列向量x1和x2张成，假设只有两维）上的投影。(求解最优w实际上用到了最小二乘法的思想)
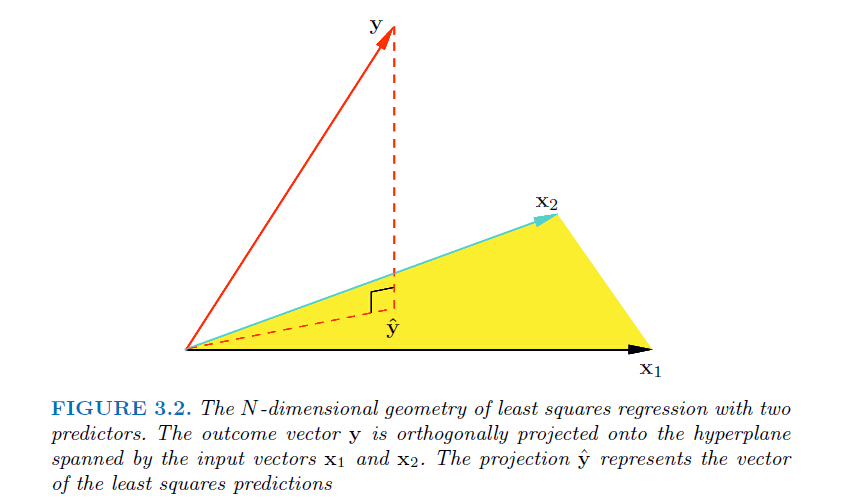
线性回归到这里就结束了，其重点在于如何通过损失函数找到最优的特征值w，当然如果求逆不好求的话我们可以通过梯度下降等优化方法来求最优解,接下来我会介绍几种优化方法。
参考链接：《learning from data》Yaser S.Abu-Mostafa
https://blog.csdn.net/xbinworld/article/details/43919445