平衡二叉树
- 概念
平衡二叉树是基于二分法的策略提高数据的查找速度的二叉树的数据结构; - 特点
平衡二叉树是采用二分法思维把数据按规则组装成一个树形结构的数据,用这个树形结构的数据减少无关数据的检索,大大的提升了数据检索的速度;平衡二叉树的数据结构组装过程有以下规则:
(1)非叶子节点只能允许最多两个子节点存在。
(2)每一个非叶子节点数据分布规则为左边的子节点小当前节点的值,右边的子节点大于当前节点的值(这里值是基于自己的算法规则而定的,比如hash值);
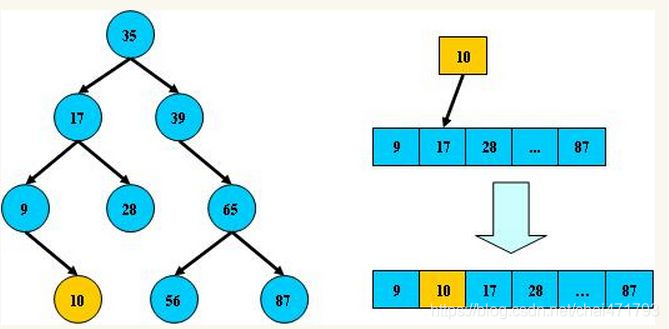
平衡树的层级结构:因为平衡二叉树查询性能和树的层级(h高度)成反比,h值越小查询越快、为了保证树的结构左右两端数据大致平衡降低二叉树的查询难度一般会采用一种算法机制实现节点数据结构的平衡,实现了这种算法的有比如Treap、红黑树,使用平衡二叉树能保证数据的左右两边的节点层级相差不会大于1.,通过这样避免树形结构由于删除增加变成线性链表影响查询效率,保证数据平衡的情况下查找数据的速度近于二分法查找;
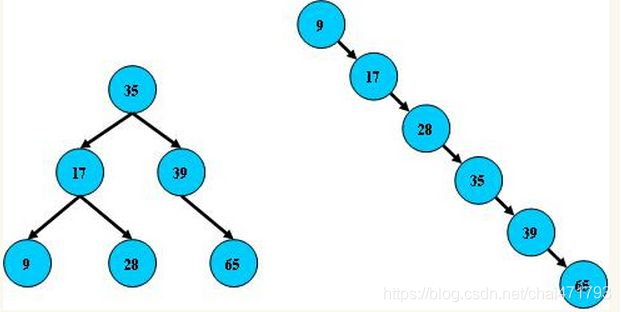
总结平衡二叉树特点:
(1)非叶子节点最多拥有两个子节点;
(2)非叶子节值大于左边子节点、小于右边子节点;
(3)树的左右两边的层级数相差不会大于1;
(4)没有值相等重复的节点;
B树
注意:之前有看到有很多文章把B树和B-tree理解成了两种不同类别的树,其实这两个是同一种树;
-
概念
B树和平衡二叉树稍有不同的是B树属于多叉树又名平衡多路查找树(查找路径不只两个),数据库索引技术里大量使用者B树和B+树的数据结构,让我们来看看他有什么特点; -
规则
(1)排序方式:所有节点关键字是按递增次序排列,并遵循左小右大原则;
(2)子节点数:非叶节点的子节点数>1,且<=M ,且M>=2,空树除外(注:M阶代表一个树节点最多有多少个查找路径,M=M路,当M=2则是2叉树,M=3则是3叉);
(3)关键字数:枝节点的关键字数量大于等于ceil(m/2)-1个且小于等于M-1个(注:ceil()是个朝正无穷方向取整的函数 如ceil(1.1)结果为2);
(4)所有叶子节点均在同一层、叶子节点除了包含了关键字和关键字记录的指针外也有指向其子节点的指针只不过其指针地址都为null对应下图最后一层节点的空格子;
最后我们用一个图和一个实际的例子来理解B树(这里为了理解方便我就直接用实际字母的大小来排列C>B>A)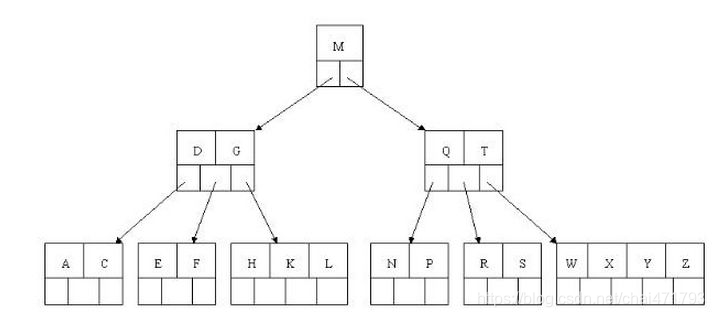
-
B树查询流程
如上图我要从上图中找到E字母,查找流程如下
(1)获取根节点的关键字进行比较,当前根节点关键字为M,E<M(26个字母顺序),所以往找到指向左边的子节点(二分法规则,左小右大,左边放小于当前节点值的子节点、右边放大于当前节点值的子节点);
(2)拿到关键字D和G,D<E<G 所以直接找到D和G中间的节点;
(3)拿到E和F,因为E=E 所以直接返回关键字和指针信息(如果树结构里面没有包含所要查找的节点则返回null);
- B树插入节点流程
定义一个5阶树(平衡5路查找树;),现在我们要把3、8、31、11、23、29、50、28 这些数字构建出一个5阶树出来;
遵循规则:
(1)节点拆分规则:当前是要组成一个5路查找树,那么此时m=5,关键字数必须<=5-1(这里关键字数>4就要进行节点拆分);
(2)排序规则:满足节点本身比左边节点大,比右边节点小的排序规则;
先插入 3、8、31、11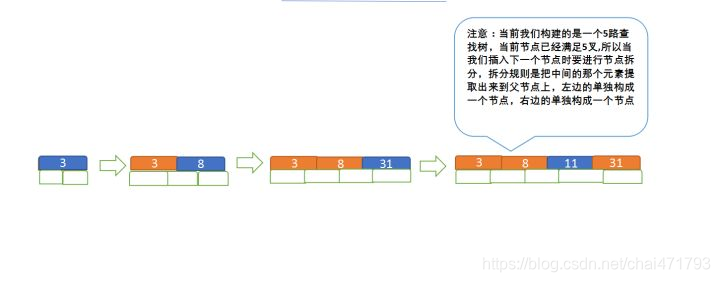
再插入23、29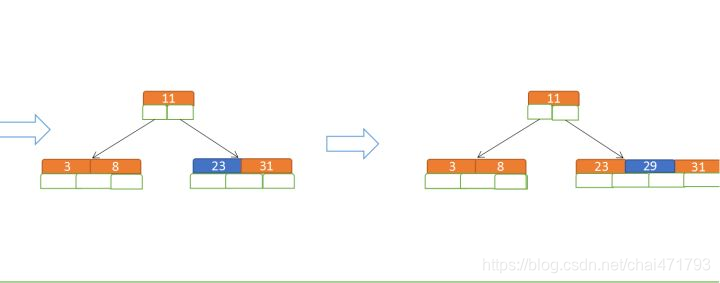
再插入50、28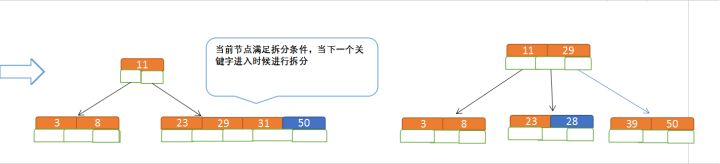
-B树节点删除
规则:
(1)节点合并规则:当前是要组成一个5路查找树,那么此时m=5,关键字数必须大于等于ceil(5/2)(这里关键字数<2就要进行节点合并);
(2)满足节点本身比左边节点大,比右边节点小的排序规则;
(3)关键字数小于二时先从子节点取,子节点没有符合条件时就向向父节点取,取中间值往父节点放;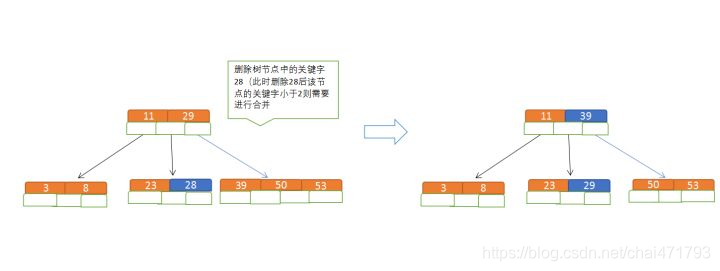
特点:
B树相对于平衡二叉树的不同是,每个节点包含的关键字增多了,特别是在B树应用到数据库中的时候,数据库充分利用了磁盘块的原理(磁盘数据存储是采用块的形式存储的,每个块的大小为4K,每次IO进行数据读取时,同一个磁盘块的数据可以一次性读取出来)把节点大小限制和充分使用在磁盘快大小范围;把树的节点关键字增多后树的层级比原来的二叉树少了,减少数据查找的次数和复杂度;
B+树
-
概念
B+树是B树的一个升级版,相对于B树来说B+树更充分的利用了节点的空间,让查询速度更加稳定,其速度完全接近于二分法查找。为什么说B+树查找的效率要比B树更高、更稳定;我们先看看两者的区别 -
规则
(1)B+跟B树不同B+树的非叶子节点不保存关键字记录的指针,只进行数据索引,这样使得B+树每个非叶子节点所能保存的关键字大大增加;
(2)B+树叶子节点保存了父节点的所有关键字记录的指针,所有数据地址必须要到叶子节点才能获取到。所以每次数据查询的次数都一样;
(3)B+树叶子节点的关键字从小到大有序排列,左边结尾数据都会保存右边节点开始数据的指针。
(4)非叶子节点的子节点数=关键字数(来源百度百科)(根据各种资料 这里有两种算法的实现方式,另一种为非叶节点的关键字数=子节点数-1(来源维基百科),虽然他们数据排列结构不一样,但其原理还是一样的Mysql 的B+树是用第一种方式实现);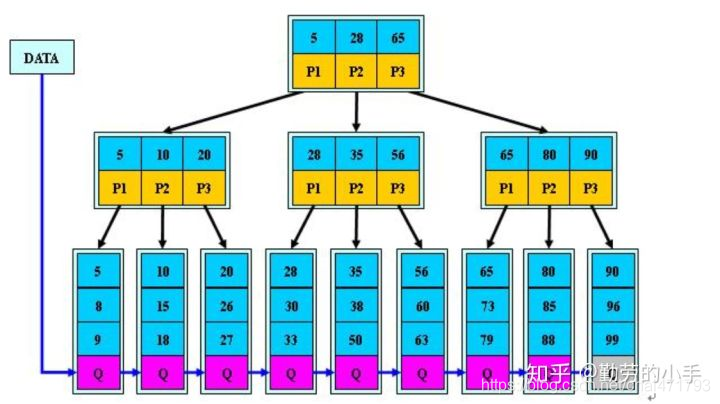 百度百科示意图
百度百科示意图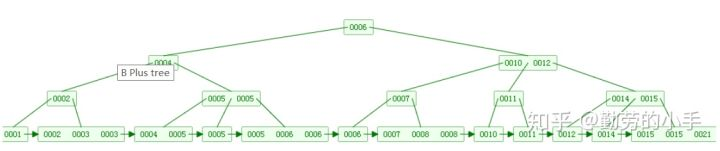 维基百科示意图
维基百科示意图 -
特点
1、B+树的层级更少:相较于B树B+每个非叶子节点存储的关键字数更多,树的层级更少所以查询数据更快;
2、B+树查询速度更稳定:B+所有关键字数据地址都存在叶子节点上,所以每次查找的次数都相同所以查询速度要比B树更稳定;
3、B+树天然具备排序功能:B+树所有的叶子节点数据构成了一个有序链表,在查询大小区间的数据时候更方便,数据紧密性很高,缓存的命中率也会比B树高。
4、B+树全节点遍历更快:B+树遍历整棵树只需要遍历所有的叶子节点即可,,而不需要像B树一样需要对每一层进行遍历,这有利于数据库做全表扫描。
B树相对于B+树的优点是,如果经常访问的数据离根节点很近,而B树的非叶子节点本身存有关键字其数据的地址,所以这种数据检索的时候会要比B+树快。
二叉查找树
要想了解二叉查找树,我们首先看下二叉查找树有哪些特性呢?
1, 左子树上所有的节点的值均小于或等于他的根节点的值
2, 右子数上所有的节点的值均大于或等于他的根节点的值
3, 左右子树也一定分别为二叉排序树
我们来看下图的这棵树,他就是典型的二叉查找树
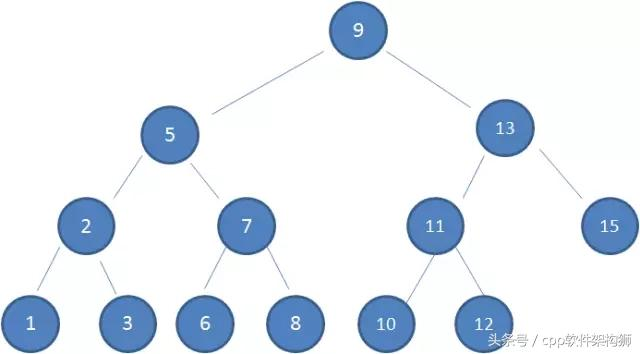
那问题来了,为什么一定要这种结构呢?换句话说这样的结构有什么好处呢?我们就来查找下值为10的节点。它怎么一步步的找到这个节点的?步骤是怎样的?接着往下看。
1, 查找到根节点9,看下图:
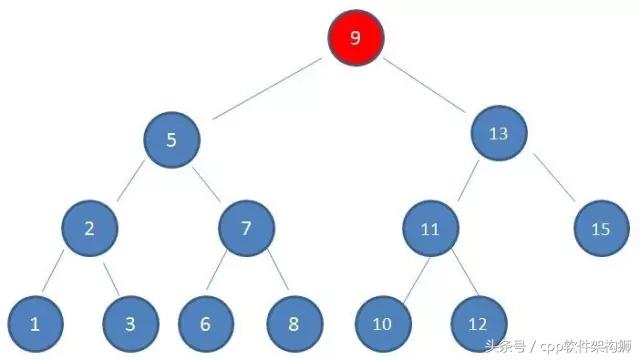
2, 由于10大于9的,所以查找到右孩子13,看下图:
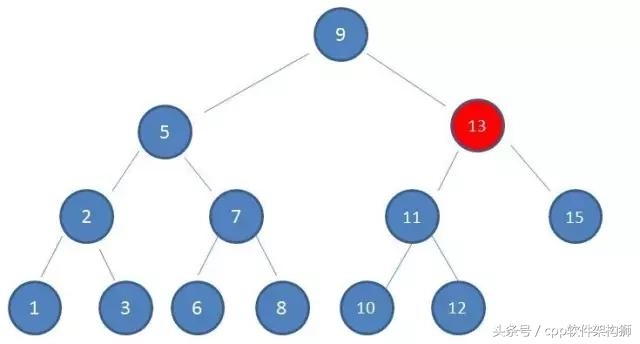
3, 又因为10是小与13的,所以查找到左孩子11,看下图:
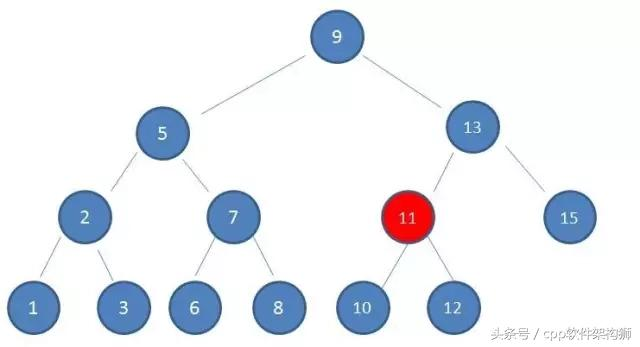
4, 这一步相比不用说了大家也都知道了,找到了左孩子,然后发现正好是10 。恰好是正要寻找的值。
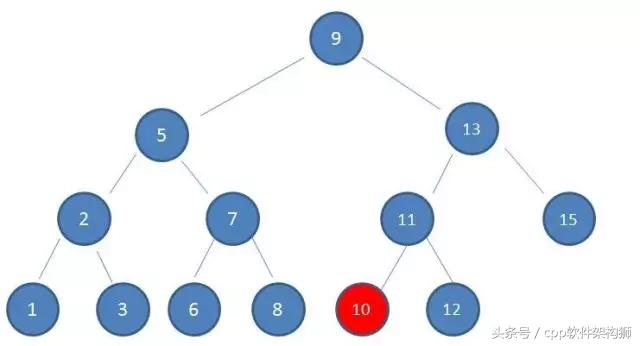
可能又有童鞋会问,这不是二分查找的思想吗?确实,查找所需的最大次数等同于二叉查找树的高度。当然在插入节点的时候,也是这种思想,一层一层的找到合适的位置插入。但是二叉查找树有个比较大的缺陷,而且这个缺陷会影响到他的性能。我们先来看下有一种情况的插入操作:
如果初始的二叉查找树只有三个节点,如下图:
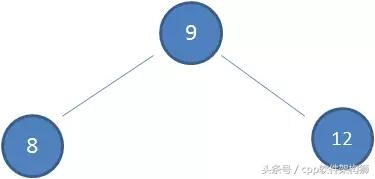
我们依次插入5个节点:7,6,5,4,3,。看下图插入之后的图:
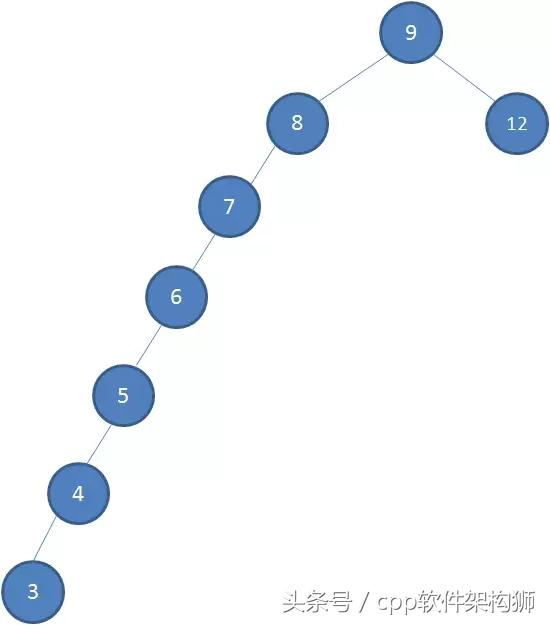
看出来了吗?有没有觉得很别扭,如果根节点足够大,那是不是“左腿”会变的特别长,也就是说查找的性能大打折扣,几乎就是线性查找了。
那有没有好的办法解决这个问题呢?解决这种多次插入新节点而导致的不平衡?这个时候红黑树就登场了。
红黑树
红黑树就是一种平衡的二叉查找树,说他平衡的意思是他不会变成“瘸子”,左腿特别长或者右腿特别长。除了符合二叉查找树的特性之外,还具体下列的特性:
1. 节点是红色或者黑色
2. 根节点是黑色
3. 每个叶子的节点都是黑色的空节点(NULL)
4. 每个红色节点的两个子节点都是黑色的。
5. 从任意节点到其每个叶子的所有路径都包含相同的黑色节点。
看下图就是一个典型的红黑树:

正是因为这些规则,才能保证红黑树的自平衡。最长路径不超过最短路径的2倍。
当插入和删除节点,就会对平衡造成破坏,这时候需要对树进行调整,从而重新达到平衡。那什么情况下会破坏红黑树的规则呢?
1,我们看下图:
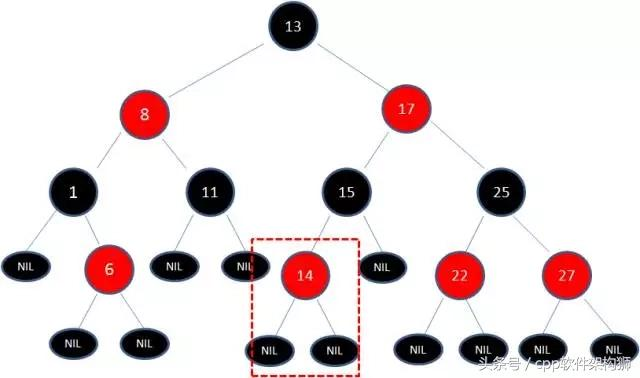
向原来的红黑树插入值为14的新节点,由于父节点15是黑色节点,所以这种情况没有破坏结构,不需要做任何的改变。
2,向原树插入21呢?,看下图:
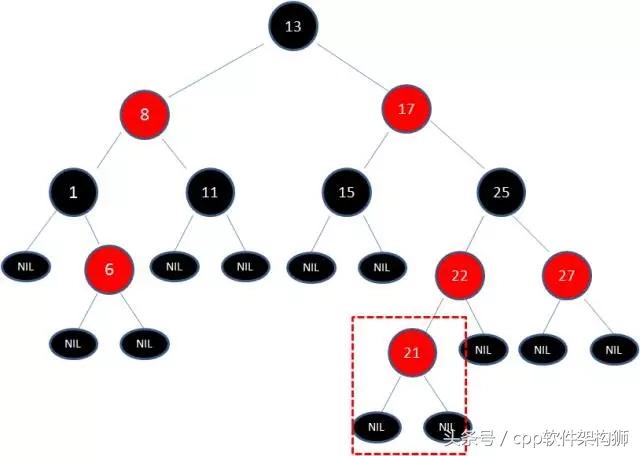
由于父节点22是红色节点,因此这种情况打破了红黑树的规则4,必须作出调整。那么究竟该怎么调整呢?有两种方式【变色】和【旋转】分为【左旋转】和【右旋转】。
【变色】:
为了符合红黑树的规则,会把节点红变黑或者黑变红。下图展示的是红黑树的部分,需要注意节点25并非根节点。因为21和22链接出现红色,不符合规则4,所以把22红变黑:
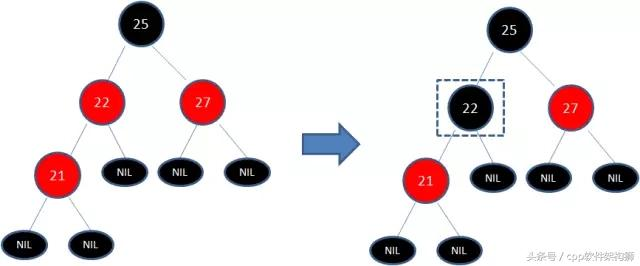
但这样还是不符合规则5,所以需要把25黑变红,看下图:
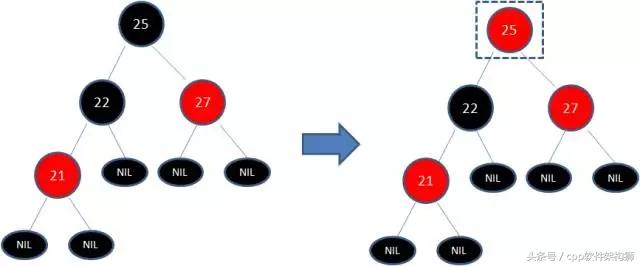
你以为现在结束了?天真,因为25和27又是两个连续的红色节点(规则4),所以需要将27红变黑。
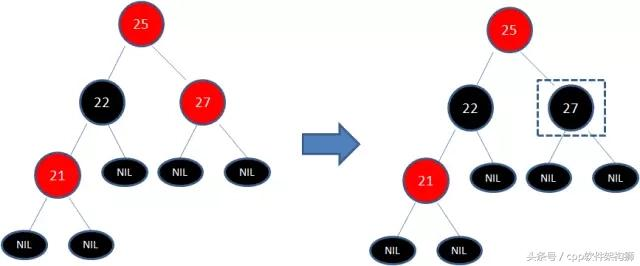
终于结束了,都满足规则了,舒服多了。
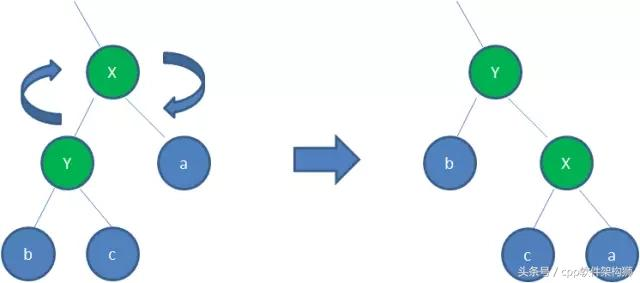
【左旋转】
也就是逆时针旋转两个节点,使父节点被自己的右孩子取代,而自己成为自己的左孩子,听起来吓死人,直接看图吧:

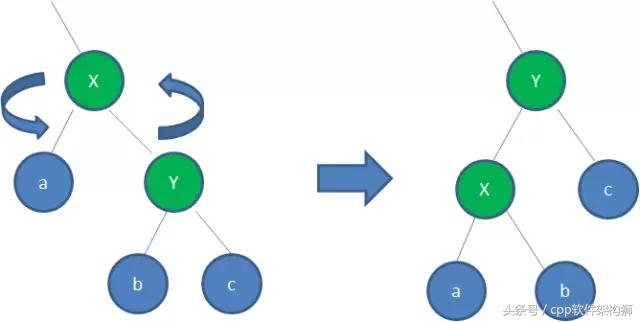
【右旋转】
顺时针旋转两个节点,使得自己的父节点被左孩子取代,而自己成为自己的右孩子,看不懂直接看图吧:
看起来这么复杂,到底怎么用呢?确实很复杂,我们讲下典型的例子,大家参考下:
以刚才插入21节点的例子:

首先我们需要做的是变色,把节点25以及下方的节点变色:

由于17和25是连续的两个红色节点,那么吧节点17变黑吗?这样是不行的,你想这样一来不就打破了规则4了吗,而且根据规则2,也不可能吧13变成红色。变色已经无法解决问题了,所以只能进行旋转了。13当成X,17当成Y,左旋转试试看:
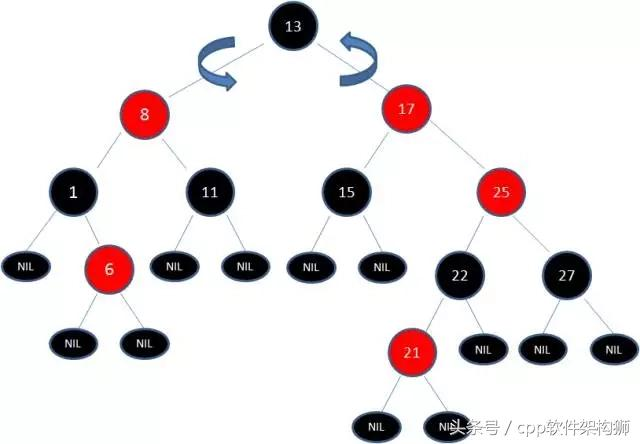

由于根节点必须是黑色,所以需要变色,结果如下图:
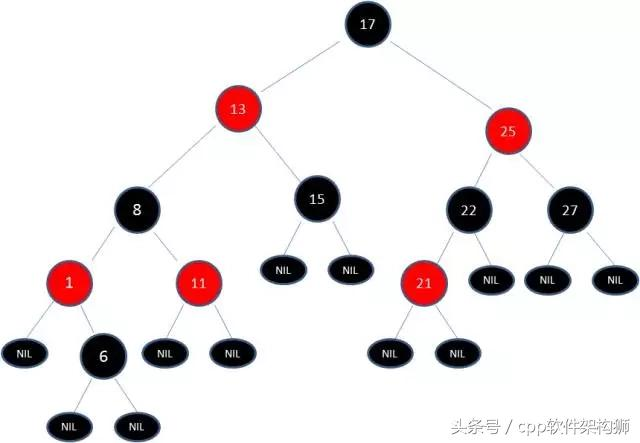
继续,其中有两条路径(17-)8->6->NULL)的黑色节点个数不是3,是4不符合规则。
这个时候需要把13当做X,8当做Y,进行右旋转:



最后根据规则变色:

红黑树和AVL树的区别:
首先红黑树是不符合AVL树的平衡条件的,即每个节点的左子树和右子树的高度最多差1的二叉查找树。但是提出了为节点增加颜色,红黑是用非严格的平衡来换取增删节点时候旋转次数的降低,任何不平衡都会在三次旋转之内解决,而AVL是严格平衡树,因此在增加或者删除节点的时候,根据不同情况,旋转的次数比红黑树要多。所以红黑树的插入效率更高。
红黑树的查询性能略微逊色于AVL树,因为他比avl树会稍微不平衡最多一层,也就是说红黑树的查询性能只比相同内容的avl树最多多一次比较,但是,红黑树在插入和删除上完爆avl树,avl树每次插入删除会进行大量的平衡度计算,而红黑树为了维持红黑性质所做的红黑变换和旋转的开销,相较于avl树为了维持平衡的开销要小得多
参考: