参考书《数据压缩导论(第4版)》 Page 100
5、给定如表4-9所示的概率模型,求出序列a1a1a3a2a3a1 的实值标签。

答: 由题意可得:对符号集A={a1,a2,a3}有:P(a1)=0.2 P(a2)=0.3 P(a3)=0.5
求序列a1a1a3a2a3a1 的实值标签就是求序列113231的实值标签。
设序列的起始上界为“1”,下界为“0”
又由于P(x=i)=P(ai),所以P(x=1)=P(a1)=0.2,
P(x=2)= P(a2)=0.3,
P(x=3)=P(a3)=0.5.
Fx(0)=0, Fx(1)=P(a0)+ P(a1)=0.2, Fx(2)=P(a1)+ P(a2)=0.5, Fx(3)=P(a1)+ P(a2)+P(a3)=1
根据公式,L(n)=L(n-1)+(U(n-1)-L(n-1))Fx(xn-1)
u(n)=L(n-1)+(U(n-1)-L(n-1))Fx(xn)
该序列第一次出现的为a1
L(1)=L(0)+(U(0)-L(0))Fx(0)=0+(1-0)*0=0
U(1)=L(0)+(U(0)-L(0))Fx(1)==0+(1-0)*0.2=0.2
该序列第二次出现的为a1
L(2)=L(1)+(U(1)-L(1))Fx(0)=0+(0.2-0)*0=0
U(2)=L(1)+(U(1)-L(1))Fx(1)=0+(0.2-0)*0.2=0.04
该序列第三次出现的为a3
L(3)=L(2)+(U(2)-L(2))Fx(2)=0+(0.04-0)*0.5=0.02
U(3)=L(2)+(U(2)-L(2))Fx(3)=0+(0.04-0)*1=0.04
该序列第四次出现的为a2
L(4)=L(3)+(U(3)-L(3))Fx(1)=0.02+(0.04-0.02)*0.2=0.024
U(4)=L(3)+(U(3)-L(3))Fx(2)=0.02+(0.04-0.02)*0.5 =0.03
该序列第五次出现的为a3
L(5)=L(4)+(U(4)-L(4))Fx(2)=0.02+(0.04-0.02)*0.2=0.024+(0.03-0.024)*0.5=0.027
U(5)=L(4)+(U(4)-L(4))Fx(3)=0.02+(0.04-0.02)*0.5 =0.024+(0.03-0.024)*1=0.03
该序列第六次出现的为a1
L(6)=L(5)+(U(5)-L(5))Fx(0)=0.027+(0.03-0.027)*0=0.027
U(6)=L(5)+(U(5)-L(5))Fx(1)=0.027+(0.03-0.027)*0.2=0.0276
所以,序列a1a1a3a2a3a1的实值标签为:T(113231)=(L(6)+ U(6))/2=0.0273;
6、对于表4-9所示的概率模型,对于一个标签为0.63215699的长度为10的序列进行解码。
答:由概率模型可知:
Fx(1)=P(a0)+ P(a1)=0.2, Fx(2)=P(a1)+ P(a2)=0.5, Fx(3)=P(a1)+ P(a2)+P(a3)=1
源程序为:
#include<iostream> using namespace std; int main() { double u[11],l[11],F[4];; u[0]=1;l[0]=0; F[0]=0;F[1]=0.2;F[2]=0.5;F[3]=1; double x=0.63215699; for(int i=1;i<11;i++) { for(int j=1;j<4;j++) { l[i]=l[i-1]+(u[i-1]-l[i-1])*F[j-1]; u[i]=l[i-1]+(u[i-1]-l[i-1])*F[j]; if(x>=l[i]&&x<u[i]) { printf("%d ",j); break; } } } return 0; }
输出结果为:
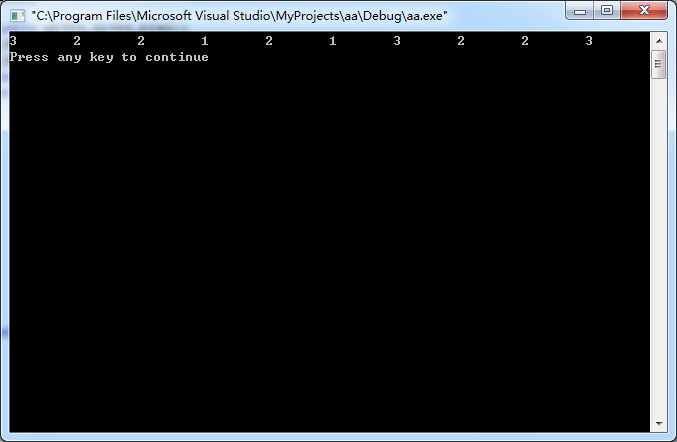
因此该标签解码后的序列为:
a3a2a2a1a2a1a3a2a2a3