原文转载自:http://blog.csdn.net/lsjseu/article/details/9990539
偶然看见了人家的博客发现这么一个问题,研究了一下午, 才发现其中的奥妙。Stupid。
题目描述:
回文串就是一个正读和反读都一样的字符串,比如“level”或者“noon”等等就是回文串。
回文子串,顾名思义,即字符串中满足回文性质的子串。
给出一个只由小写英文字符a,b,c…x,y,z组成的字符串,请输出其中最长的回文子串的长度。
输入:
输入包含多个测试用例,每组测试用例输入一行由小写英文字符a,b,c…x,y,z组成的字符串,字符串的长度不大于200000。
输出:
对于每组测试用例,输出一个整数,表示该组测试用例的字符串中所包含的的最长回文子串的长度。
样例输入:
abab
bbbb
abba
样例输出:
3
4
4
思路:
回文串包括奇数长的和偶数长的,一般求的时候都要分情况讨论,这个算法做了个简单的处理把奇偶情况统一了。原来是奇数长度还是奇数长度,偶数长度还是偶数长度。
算法的基本思路是这样的,把原串每个字符中间用一个串中没出现过的字符分隔#开来(统一奇偶),同时为了防止越界,在字符串的首部也加入一个特殊符$,但是与分隔符不同。同时字符串的末尾也加入’�’.
算法的核心:用辅助数组p记录以每个字符为核心的最长回文字符串半径。也就是p[i]记录了以str[i]为中心的最长回文字符串半径。p[i]最小为1,此时回文字符串就是字符串本身。
先看个例子:
原串: w aa bwsw f d
新串: $ # w# a # a # b# w # s # w # f # d #
辅助数组P: 1 2 1 2 3 2 1 2 1 2 1 4 1 2 1 2 1 2 1
首先看代码(借助http://blog.csdn.net/thyftguhfyguj/article/details/9531149):
#include <stdio.h>
#include <iostream>
using namespace std;
char s[200002];
char str[400010];
int p[400010];
int min(int a,int b){
return a < b ? a : b;
}
int pre(){
int i,j = 0;
str[j++] = '$';//加入字符串首部的字符串
for(i = 0;s[i];i++){
str[j++] = '#'; //分隔符
str[j++] = s[i];
}
str[j++] = '#';
str[j] = '�'; //尾部加'�'
cout<<str<<endl;
return j;
}
void manacher(int n){
int mx = 0,id,i;
p[0] = 0;
for(i = 1;i < n;i++){
if(mx > i) //在这个之类可以借助前面算的一部分
p[i] = min(mx - i,p[2 * id - i]); //p[2*id-i]表示j处的回文长度
else //如果i大于mx,则必须重新自己算
p[i] = 1;
while(str[i - p[i]] == str[i + p[i]]) //算出回文字符串的半径
p[i]++;
if(p[i] + i > mx){ //记录目前回文字符串扩展最长的id
mx = p[i] + i;
id = i;
}
}
}
int main(int argc, char const *argv[]){
while(scanf("%s",s) != EOF){
int n = pre();
manacher(n);
int ans = 0,i;
for(i = 1;i < n;i++)
if(p[i] > ans)
ans = p[i];
printf("%d
",ans - 1);
}
return 0;
} 上面的程序说明:pre()函数对给定字符串进行预处理,也就是加分隔符。
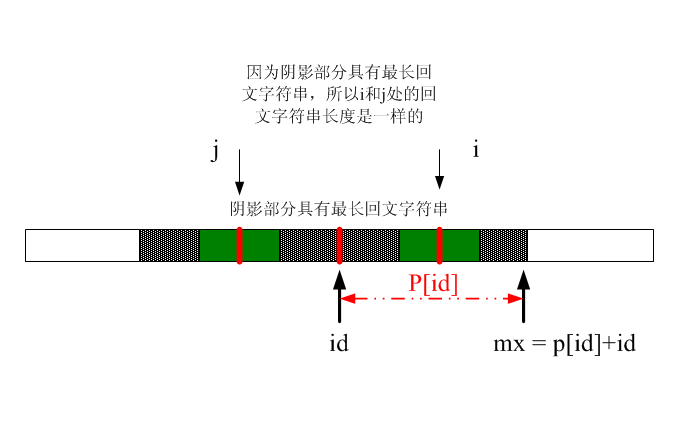
上面几个变量说明:id记录具有遍历过程中最长半径的回文字符串中心字符串。mx记录了具有最长回文字符串的右边界。看下面这个图(注意,j为i关于id对称的点,j = 2*id - i):
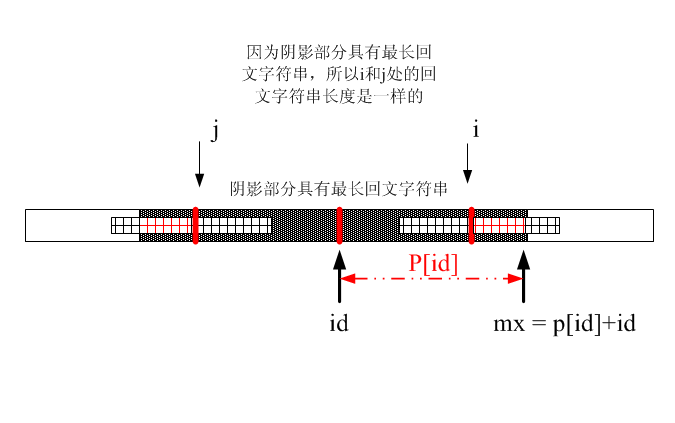
但是p[i] = p[j]是没有错的,但是这里有个问题,就是i的一部分超出阴影部分,这就不对了。请看下图(为了看得更清楚,下面子串用细条纹表示):
此时,根据对称型只能得出p[i]和p[j]红色阴影部分是相等的,这就为什么有取最小值这个操作:
if(mx > i) //在这个之类可以借助前面算的一部分
p[i] = min(mx - i,p[2 * id - i]); 下面代码就很容易看懂了。
最后遍历一遍p数组,找出最大的p[i]-1就是所求的最长回文字符串长度,下面证明一下:
(1)因为p[i]记录插入分隔符之后的回文字符串半径,注意插入分隔符之后的字符串中的回文字符串肯定是奇数长度,所以以i为中心的回文字符串长度为2*p[i]-1。
例如:
bb=>#b#b#
bab=>#b#a#a#b#
2)注意上面两个例子的关系。#b#b#减去一个#号的长度就是原来的2倍。即((2*p[i]-1)-1)/2 = p(i)-1,得证。
算法的有效比较次数为MaxId 次,所以说这个算法的时间复杂度为O(n)。