1. K-Means 算法
此算法是很常用的一个算法,也是基于向量距离来做聚类。算法步骤:
(1) 从 n 个向量对象任意选择 k 个向量作为初始聚类中心
(2) 根据在步骤(1)中设置的 k 个向量(中心对象向量),计算每个对象与这 k 个中心对象各自的距离
(3) 对于步骤(2)中的计算,任何一个向量与这 k 个向量都有一个距离,有的远,有的近,把这个向量和距离它最近的中心向量对象归在一个类簇中。
(4) 重新计算每个类簇的中心对象向量位置
(5) 重复(3)(4)两个步骤,直到类簇聚类方案中的向量归类变化极少为止。例如,一次迭代后,只有少于1%的向量还在发生类簇之间的归类漂移。
2. 有趣模式
如果一个模式具备以下特点,那么它是有趣的:
(1)易于被人理解。
(2)在某种确信度上,对于新的或检验数据是有效的。
(3) 是潜在有用的
(4)是新颖的。
3. 孤立点
在聚类的过程中,会常常碰到一些离主群或者离每个群都非常远的点,这种点叫作孤立点。孤立点通常也是有具体意义的。孤立点通常由一些和群里的个体特点差异极大的样本组成。对孤立点的研究也有实际意义。如信用卡诈骗。
4. 层次聚类
K-Means 算法是直接把样本分成若干个群,而现在讨论的层次聚类就是通过聚类算法把样本根据距离分成若干大群,大群之间相异、大群内部相似,而大群内部又当成一个全局的样本空间,再继续划分若干小群,小群之间相异、小群内部相似。这就是层次聚类的思想。最后形成的是一棵树的结构。
5. 密度聚类
密度聚类很多时候用在聚类形状不规则的情况下。
6. 聚类评估
评估聚类算法的好坏。
聚类的质量评估包括:
(1) 估计聚类的趋势。对于给定的数据集,评估该数据集是否存在非随机结构,也就是分布不均匀的情况。
使用霍普金斯统计量来估算是否有聚类的趋势。步骤:
(a)从所有样本中随机选取 n 个向量,对每个向量在样本空间里找一个离其最近的向量,然后求距离(用欧氏距离即可),用 X1,X2....,Xn 表示这些距离。
(b)重复上面的步骤,用 Y1, Y2,..., Yn 表示这些距离
(c)用下面的公式计算霍普金斯统计量 H。如果一个样本空间是均匀的(即没有聚类趋势),则 H 值为 0.5左右。反之应该接近1。

(2) 确定数据集中的簇数。上述 K-Means 算法在一开始就需要确定类簇的数量,并作为参数传递给算法。这里容易让人觉得有点矛盾,即人主观来决定一个类簇的数量的方法是不是可取。
有一种简单的经验法作为参考:对 n 个样本的空间,设置簇数 p 为 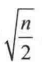 , 在期望状态下每个簇大约有
, 在期望状态下每个簇大约有 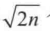 个点。
个点。
更为科学的方法 -- 肘方法( The Elbow Method)
(3) 测量聚类的质量。
外在方法: 一种依靠类别基准的方法。即已经有比较严格的类别定义时再讨论聚类是不是足够准确。通常使用"BCubed精度" 和 "BCubed召回率"
内在方法:不会参考类簇的标准,而是使用轮廓系数进行度量。
对于有 n 个向量的样本空间,假设它被划分中 k 个类簇,即 C1,C2... Ck。对于任何一个样本空间中的向量 v 来说,可以求一个 v 到 本类簇中其他各点的距离的平均值 a(v),还可以求一个 v 到其它所有各类簇的最小平均距离(即从每个类簇里挑选一个离 v 最近的向量,然后计算距离),求这些距离的平均值,得到 b(v),轮廓系数定义为:
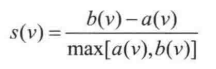
一般来说,这个函数的结果在 -1 和 1 之间。 a(v) 表示的是类簇内部的紧凑型,越小越紧凑,而 b(v) 表示该类簇和其他类簇之间的分离程度。如果函数接近1,即 a(v) 比较小而 b(v) 比较大时,说明包含 v 的类簇非常紧凑,而且远离其他的类簇。相反,如果函数值为负数,则说明 a(v)>b(v), v 距离其他的类簇比距离自己所在类簇的其他对象更近,那么这种情况质量就不太好,应该尽可能避免。