基于能量的模型(EBM)
基于能量的模型将每一个我们感兴趣的变量构造联系到一个标量能量上.
学习就是修改能量方程从而使得它的外形有我们需要的特点.
举例来说, 希望的是: 期望构造的能量低.
基于能量的概率性模型定义了一个概率分布, 它是由能量方程决定的:
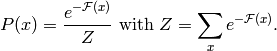(1)归一化因子Z被称为配分函数, 类比于物理系统.
基于能量的模型可以通过SGD(随机梯度下降)算法学习得到.
有隐层单元的EBM
在实际中并不能观测到样本x的所有特征, 或者需要引入一些并非观测得到的变量来增加模型的区分度(the expressive power of the model).
为了这个目的, 我们定义一个观察项x和一个隐藏项h. 从而有:
(2)ps: 上式为观察项x对模型概率分布的影响关系
为了将此式近似映射到等式(1)上, 引入自由能量(free energy)的记号(取自物理), 定义:
(3)ps: 将每个隐藏项带来的能量求和再求负对数
从而(2)式可以改写为:
从而数据的负值对数似然度(NLL)的梯度的形式特别有趣:
(4)[第一项为分子偏导, 第二项为分母偏导, 注意∂exp(-F(x))/ ∂θ = exp(-F(x)) * ∂(-F(x))/∂θ ]
注意到上述梯度包含了两部分, 分别是正向和负向分量.
这两部分并不和它们在等式中的符号对应, 但是反映了它们对于概率密度的影响.
第一部分增加了训练数据的概率(通过减少对应的自由能量), 第二部分则降低了模型产生的样本概率.
通常很难从分析这些梯度, 因为它涉及了计算![]()
梯度
.
. 这完全和从所有的可能输入x中能够获得的期望相同(在模型给定的分布P的条件下)!
解决这个问题的第一步就是使用一个固定数量的模型样本来估计期望. 用于估计负向分量梯度的样本被称为负粒子(negative particles), 使用![]()
N表示. 梯度可以表示为:
(4)理论上我们希望![]()
中的![]()
能够按照P来采样(比如做蒙特卡洛).
基于上述公式, 我们几乎已经得到了用于学习一个EBM的实用的随机算法. 唯一尚未解决的是如何提取这些负粒子![]()
.
马尔科夫链蒙特卡洛方法对于RBM模型(EBM的一种特殊情况)非常合适.
受限玻尔兹曼机(RBM)
玻尔兹曼机(BMs)是对数线性马尔科夫随机域(log-linear Markov Random Field (MRF))的一种特殊形式, 它的能量函数对于自由参数是线性的.
为了能够使得它们能够表达复杂的分布(从受限变参设置到一个非变参设置), 我们假设某些变量是从未被观察到的(隐藏的).
隐含变量(隐含单元)越多, BM模型的容量就越大.
受限BM进一步限制了BM, 它没有可见-可见或隐藏-隐藏的连接(即没有层内连接, 只有层间连接).
RBM的图示如下:
RBM的能量方程E(v, h)定义为:
其中W代表连接隐藏和可见单元的权重, b,c是可见和隐藏层的偏置.
从而可以得到下面的自由能量公式:
因为RBM的特殊结构 -- 可见和隐藏单元是相互独立的, 利用这个特性我们得到:
二进制单元的RBM
使用二进制单元的一般情况下(vj和hi∈{0, 1}), 我们可以从式(6)和(2)中得到一个似然版本的通用神经元激活函数:
(7)
(8)sigm(x) = sigmoid(x) = exp(-x)/(1+exp(-x))
RBM的自由能量则简化为:
(9)使用二进制单元更新等式
结合等式(5)和(9), 我们可以得到下列二进制单元RBM的对数相似性梯度:
(10)我们在Theano中使用T.grad对式(4)进行处理得到此式而不是直接使用.
RBM的采样
p(x)的采样可以通过运行一个马尔科夫链来收敛得到, 使用Gibbs采样作为过渡操作.
N个随机变量的Gibbs采样通过一系列形如
的N个子采样步骤(sub-step)实现, 其中
包含S中除了Si的其他N-1个随机变量.
对于RBM, S由可见和隐藏神经元集合组成, 但是因为它们是条件独立的, 所以可以进行Gibbs块采样(block Gibbs sample). 在这种条件下, 可见神经元在隐藏神经元值给定同时进行采样. 相似的, 隐藏神经元也在可见神经元值给定同时进行采样. 马尔科夫链中的一步(step)操作如下:![]()
其中![]()
h(n)代表马尔科夫链的第n步的所有隐藏神经元集合. 它的意义是, 
![]()
按照概率
![]()
随机设置为1/0, 相似的
![]()
则按照概率
![]()
随机设置为1/0. 如下图:
当![]()
, 采样对![]()
就能保证为p(v,h)的精确采样.
, 采样对就能保证为p(v,h)的精确采样.理论上, 学习过程中每次更新参数都要求运行一次这个链直到收敛. 毫无疑问这样做成本太高. 因此, 很多算法设计出来, 用于有效地在学习过程中对p(v,h)进行采样.
对比差异算法(contrastive divergence, CD-k)
CD算法使用2个技巧来加速采样过程:
- 因为最终希望
(数据的真实分布), 我们使用一个训练样本来初始化马尔科夫链(即使用一个更接近于p的分布, 从而使得链已经接近于收敛到最终分布p)
- CD并不等待链收敛, 采样点集在第k步Gibbs采样结束后就获得了. 实际应用中, k = 1效果已经非常好.
持续CD(PCD)
持续CD使用了另一种p(v,h)采样的估计. 它依赖于一个单一马尔科夫链, 该链有一个不变的状态(即并不对于每一个观测样本都重启该链). 对于每一次参数更新, 我们通过简单的运行链k步来提取新的样本. 链的状态被保存, 用于之后的更新.
基本思想是如果参数变化相对链的混合状态足够小, 马尔科夫链就能够"跟上"(“catch up”)模型的变化.
实现
实现的分析见此文:[深度学习]受限玻尔兹曼机生成手写数字训练样本实现分析.