LCA(不知道全称叫什么)
-倍增版-
作用:在一棵树中求两点公共祖先中深度最大的那个
存在一颗 n 点的树,询问 m 次两个点的最近公共祖先
复杂度:预处理O(nlogn),询问O(logn)
主要思想:倍增
预处理:
预处理出 f [ i ] [ j ] 数组,表示 i 点向上 2j 步的点,即自己往上数第 2j 个祖先
预处理出 dep [ i ] 数组,表示以第 i 个点的深度
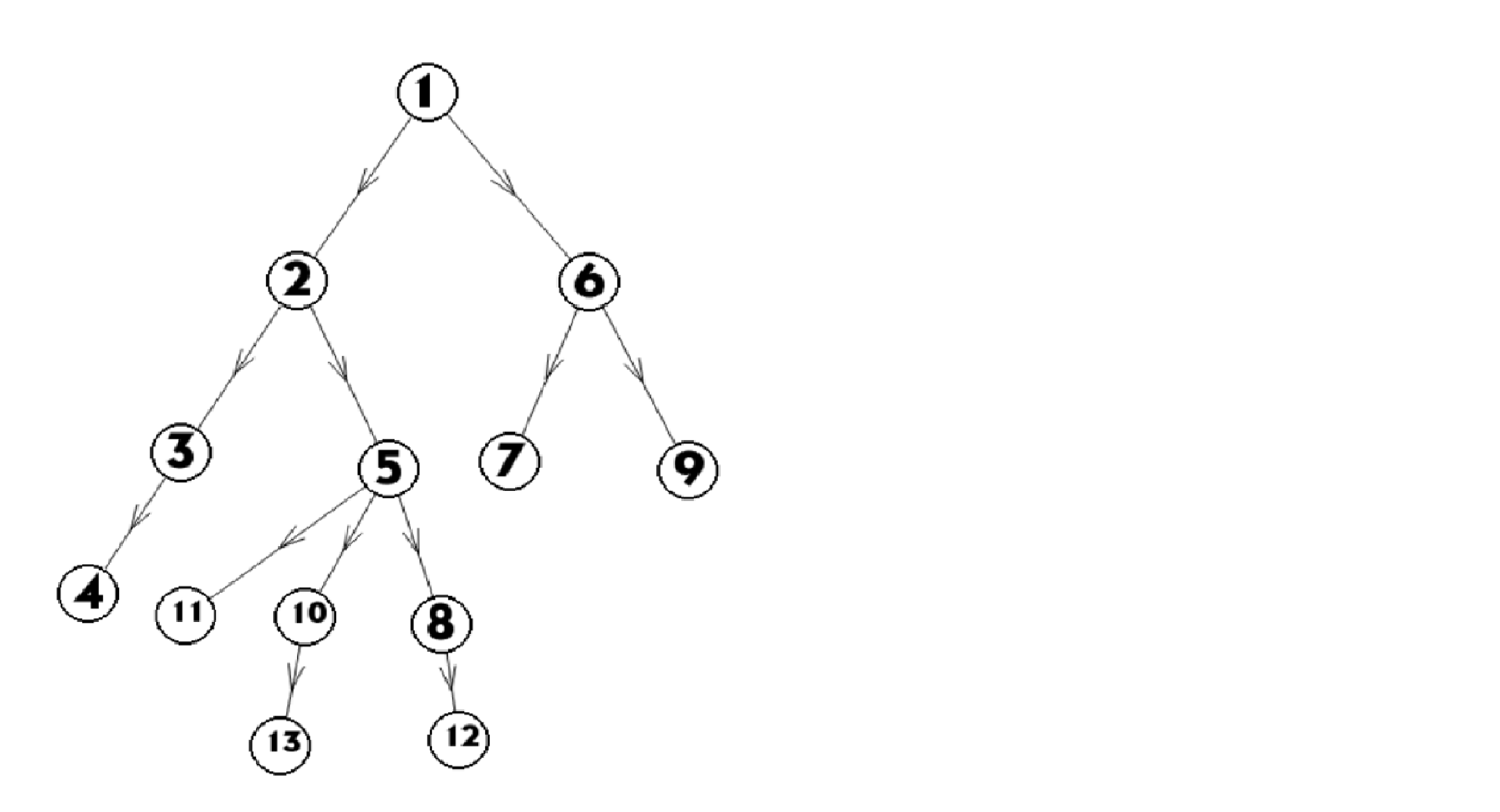
这样先给出一张以1为根的样例树,比较好解释一点,这里的值都是相对于根为1的情况,预处理的全部内容以该树为参考
那么 f [ 12 ] [ 0 ] = 8 , f [ 12 ] [ 1 ] = 5 , f [ 12 ] [ 2 ] = 1
那么 dep [ 1 ] = 1 , dep [ 5 ] = 3 , dep[ 13 ] = 5
i 点向上 2j 相当于 i 点往上数的第 2j-1 个祖先向上 2j-1 步
预处理转移方程:
for(int i=1;(1<<i)+1<=dep[u];++i) f[u][i]=f[f[u][i-1]][i-1];
dep [ ] 数组的处理用dfs完成,于是在处理dep [ ] 的同时,可以顺便处理 f [ ] [ ]数组
那么预处理只需要一个dfs即可完成。
注意很多时候给边的时候未给定边的方向(比如只说u点到v点有一条边,没说明是u到v或v到u),建边要双向,由一个根开始的dfs来确定每条边的方向。
void dfs(int u,int fa){ v[u]=true; f[u][0]=fa; dep[u]=dep[fa]+1; for(int i=1;(1<<i)+1<=dep[u];++i) f[u][i]=f[f[u][i-1]][i-1]; for(int i=head[u];i;i=edge[i].nxt) if(!v[edge[i].to]) dfs(edge[i].to,u); } int main(){ dfs(1,0); }
注意dfs中 fa 是 u 的父亲。
为什么dfs的开始可以 0 是 1 的父亲开始呢?
这样预处理难道不会出现问题吗?
还真没有,将 0 定为 1 的父亲后,由于第一个for中 (1<<i)+1<=dep[u] 所以除了 1 的点全部不会将 0 作为父亲
即使全把 0 做父亲也没有事情,因为最近公共祖先的定义保证了两个点最大的公共最先顶多是根,不会到 0
查询:
在讲查询之前先来说说倍增的思想
一个 x 个单位长的区间,可以分解为几个不同的 2k 的长度的小区间
如14可以拆成8+4+2
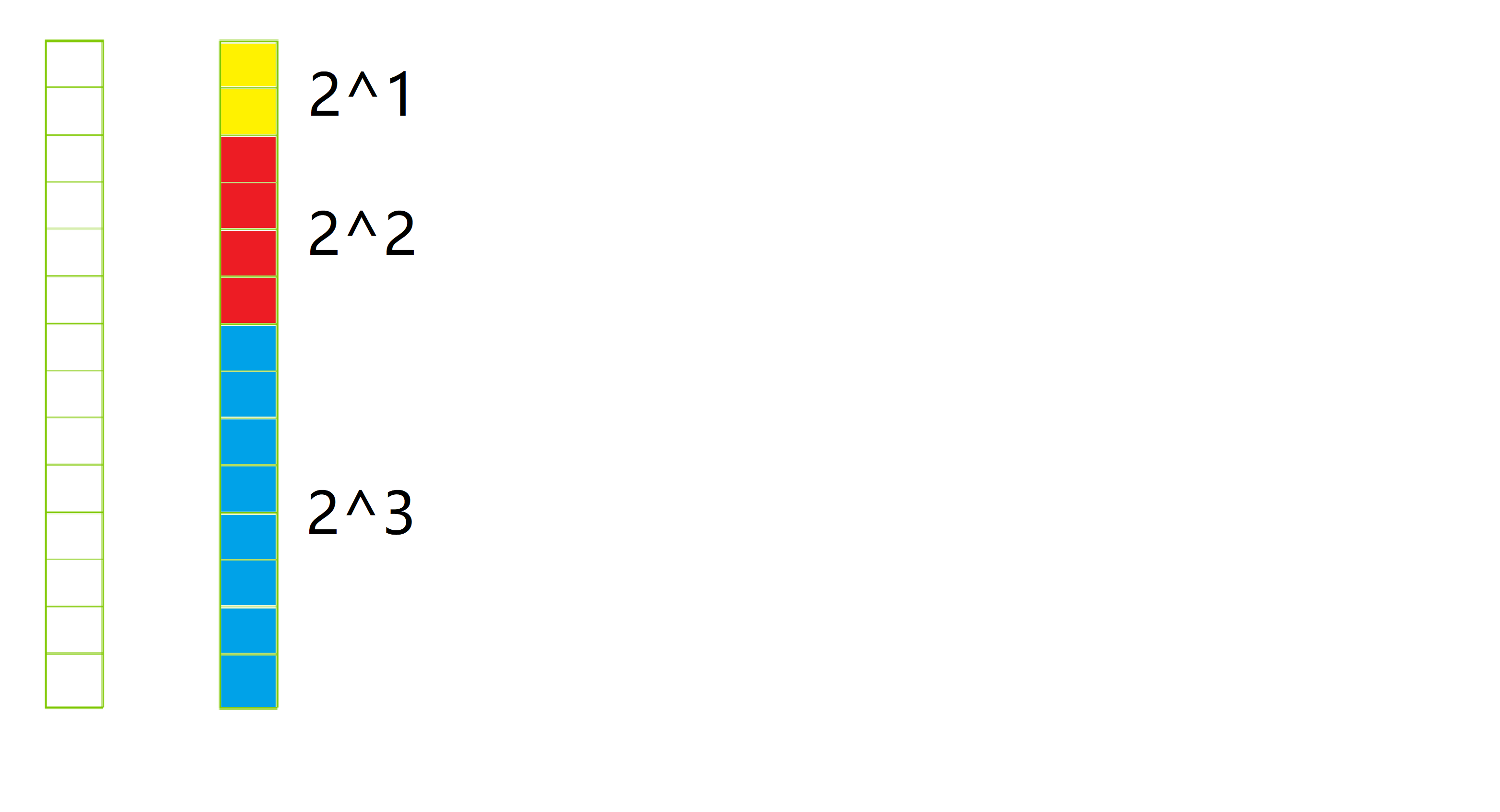
同样的,我们想到从0到14可以拆解为如上三个步骤,先走 23 步再走 22 步再走 21
相关知识可以证明这个步数的组成是不同的且唯一的 (请查阅小学奥数)
如此一来在一棵树中,求一个点往上走 q 步到达的祖先只需要 logq 的复杂度
我们考虑 x,y两点处在共同的深度时
他们有许多的公共祖先,若 f [ x ] [ k ]与f [ y ] [ k ] 相同,代表他们向上走 2k 步的点是他们的公共祖先
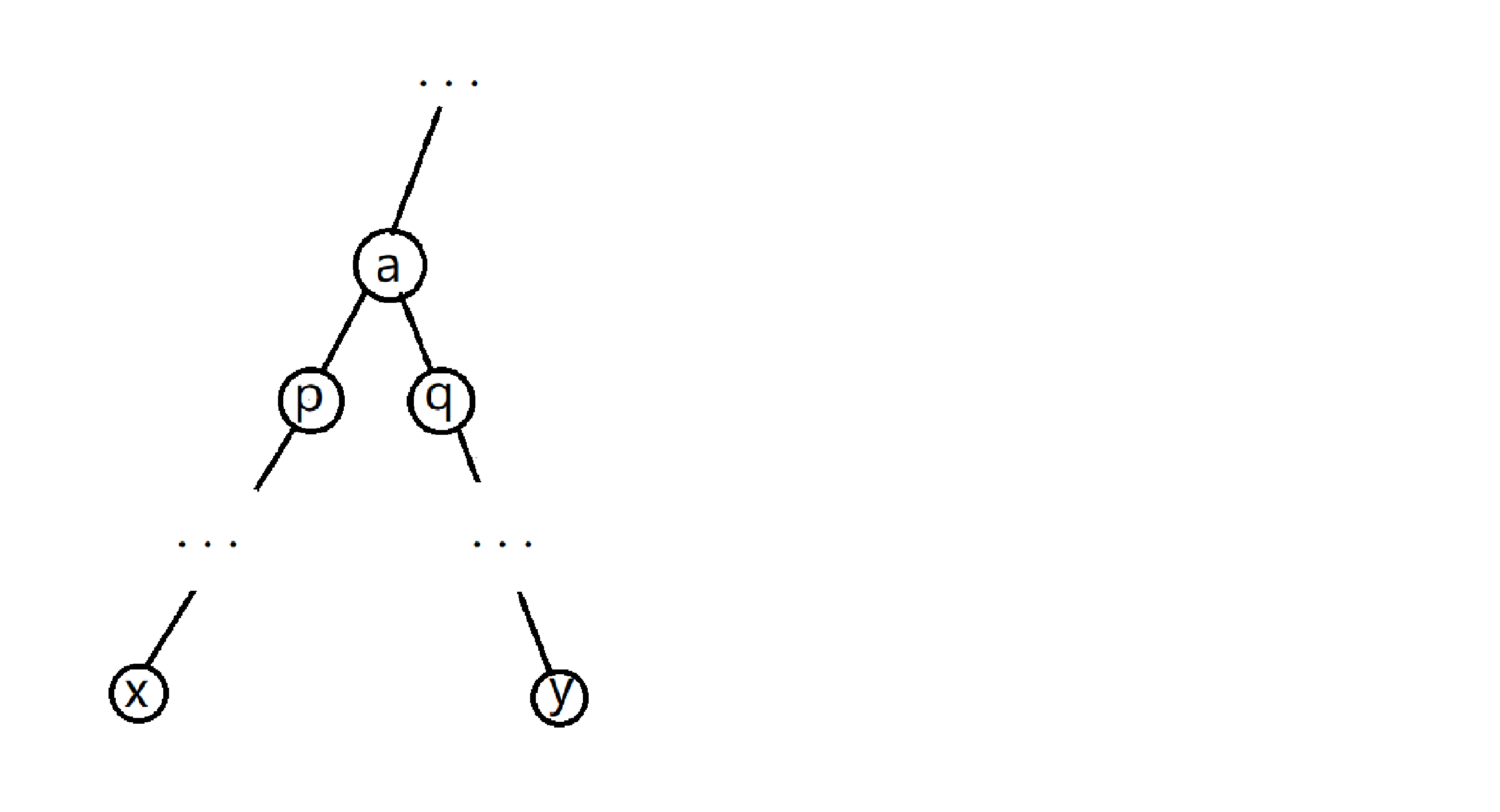
如图 a 是x、y的最近公共祖先,a的祖先都是x、y的祖先,p、q是 a 儿子且dep[p]=dep[q]=dep[a]+1
LCA的大致思想是不断更新x,y的位置,让他们向上爬,p是我们希望x最终到达的位置,q是我们希望y最终到达的位置。
我们每次确定一个值k,表示让x,y都爬 2k 步,之前说了x到p与y到q的路径可以拆分成不同的2k,所以让k改变,判断这次的k是否需要爬即可
可以发现如果走到a或a的祖先(x、y的公共祖先)时,x和y的位置变为相同,需要爬的部分在于a以下
int same_LCA(int x,int y){ int k=log2(dep[x])+1; while(k>=0){ if(f[x][k]!=f[y][k]) //本次爬完完在x~p和y~q的范围内 x=f[x][k],y=f[y][k]; //爬 --k; }
//此时的x,y即为p,q的位置 }
那么此时的fa[x][0]= p往上爬一步= a号点 =最近公共祖先
我们再考虑 x,y 不同深度
那么简单,把x,y调成同深度即可,原理与上面相同
if(dep[x]<dep[y]) swap(x,y); while(dep[x]>dep[y]){ int l=log2(dep[x]-dep[y]); x=f[x][l]; }
然后再贴个代码,模板题是[洛谷 P3379 【模板】最近公共祖先(LCA)]
#include<bits/stdc++.h> #define maxn 1000010 using namespace std; int n,m,s,edge_num; int head[maxn],f[maxn][21],father[maxn],dep[maxn]; bool v[maxn]; struct { int nxt,to; }edge[maxn]; void add_edge(int from,int to){ edge[++edge_num].nxt=head[from]; edge[edge_num].to=to; head[from]=edge_num; } void dfs(int u,int fa){ v[u]=true; f[u][0]=fa; dep[u]=dep[fa]+1; for(int i=1;(1<<i)+1<=dep[u];++i) f[u][i]=f[f[u][i-1]][i-1]; for(int i=head[u];i;i=edge[i].nxt) if(!v[edge[i].to]) dfs(edge[i].to,u); } int LCA(int x,int y){ if(dep[x]<dep[y]) swap(x,y); while(dep[x]>dep[y]){ int l=log2(dep[x]-dep[y]); x=f[x][l]; } if(x==y) return x; int k=log2(dep[x])+1; while(k>=0){ if(f[x][k]!=f[y][k]) x=f[x][k],y=f[y][k]; --k; } return f[x][0]; } int main(){ scanf("%d%d%d",&n,&m,&s); for(int i=1;i<=n-1;++i){ int u,v; scanf("%d%d",&u,&v); add_edge(u,v); add_edge(v,u); } dfs(s,0); for(int i=1;i<=m;++i){ int u,v; scanf("%d%d",&u,&v); printf("%d ",LCA(u,v)); } }