目录
第一部分 应用数学与机器学习基础
第1章 引言
人工智能的真正挑战在于解决那些对人来说很容易执行、但很难形式化描述的任务,如识别人们所说的话或图像中的脸。
深度学习:让计算机从经验中学习,并根据层次化的概念体系来理解世界,而每个概念这通过与某些相对简单的概念之间的关系来定义。
一个人的日常生活需要关于世界的巨量知识,而且大多是主观的,直观的,因此很难通过形式化的方式表达清楚。计算机需要获取同样的知识才能表现出智能。人工智能的一个关键挑战就是如何将这些非形式化的知识传达给计算机(也就是将输入表示成计算机可以理解的形式,比如提取特征,通过边缘信息让神经网络识别图像;RGB图像用0-255表示是人为定义的,原始图像所包含的信息量最多,但是却不是程序所能直接识别的,所以需要转换成它们自己的语言和形式,这些就是通过特征学习)
机器学习:早先,一些人工智能项目致力于将关于世界的知识用形式化语言进行硬编码【知识库】,人们设法设计出足够复杂的形式化规则来精确地描述世界,依靠人为设计规则很繁琐并且不够全面,因此表明,AI系统需要具备自己获取知识的能力,即从原始数据中提取模式的能力,这种能力称为机器学习。
简单的机器学习算法的性能在很大程度上依赖于给定数据的表示(特征选择),表示的选择会对机器学习算法的性能产生巨大的影响。

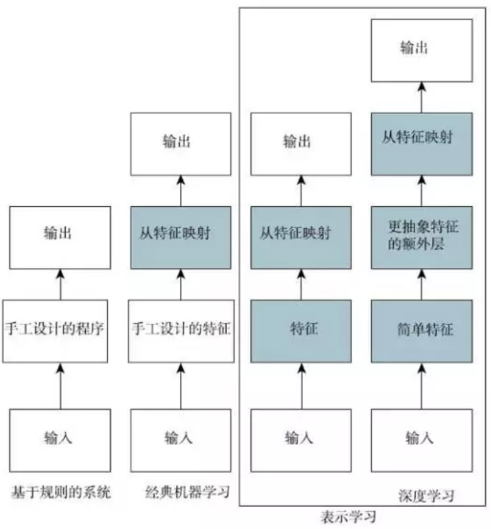
表示学习:对于许多任务来说,我们很难知道应该提取哪些特征,解决这个问题的途径之一是使用机器学习来发掘表示本身,而不仅仅把表示映射到输出。这种方法我们称之为表示学习。表示学习算法只需要几分钟就可以为简单的任务发现一个很好的特征集。
表示学习算法的典型例子是自编码器
当设计特征或设计用于学习特征的算法时,我们的目标通常是分离出能解释观察数据的变差因素(factors of variation),它们是现实世界中观察不到的物体或者不可观测的力,但会影响可观测的量。比如说,当分析语音记录时,变差因素包括说话者的年龄,性别,他们的口音和他们正在说的词语。当分析汽车的图像时,变差因素包括汽车的位置、它的颜色、太阳的角度和亮度。
在现实生活中,困难主要源于多个变差因素在同时影响着我们能够观察到的每一个数据。实际应用中就需要清理变差因素并忽略我们不关心的因素。
然而从原始数据中提取如此高层次、抽象的特征是非常困难的,比如说话口音这种变差因素,几乎与获得原问题的表示一样难,所以表示学习作用不大,深度学习通过其他较简单的表示来表达复杂表示,解决了表示学习中的核心问题。
深度学习让计算机通过较简单的概念构建复杂的概念。
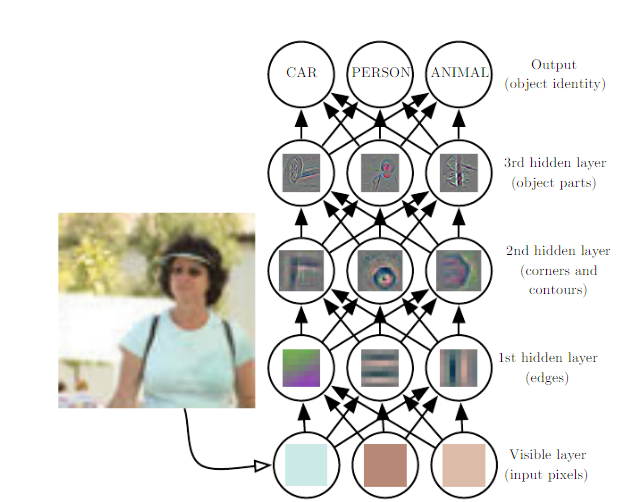
计算机难以理解原始感官输入数据的含义,如表示为像素值集合的图像。将一组像素映射到对象标识的函数非常复杂。想要直接处理几乎不可能,深度学习将所需要的复杂映射分解为一系列嵌套的简单映射(每个又模型的不同层描述)来解决这一难题
总结:
深度学习是一种特定类型的机器学习,具有强大的能力和灵活性,它将大千世界表示为嵌套的层次概念体系(由简单概念间的联系定义复杂概念、从一般抽象概括到高级抽象表示)
1.2 深度学习的历史趋势
深度学习的三次发展浪潮:
- 20世纪40年代到60年代,深度学习的雏形出现在控制论中: 生物学习理论的发展和第一个模型的实现(感知机 1958)能实现单个神经元的实现;以简单线性模型开始,称为人工神经网络ANN, 不能学习异或XOR函数,导致了第一次衰退
- 20世纪80年代到90年代,深度学习表现为联结主义:可以用反向传播(1986)训练具有一两个隐藏层的神经网络, 神经网络的达不到投资者的期望值,核方法和图模型的出现及有效应用导致了神经网络热潮的第二次衰退
- 2006年,以深度学习之名复兴,Hinton 深度置信网络 "贪婪逐层预训练" 开始成功训练深度网络
神经科学是深度学习研究的一个重要灵感来源,但它已不再是该领域的主要指导,因为我们根本没有足够的关于大脑的信息来作为指导去使用它(在神经科学方面的研究还远远不够)
研究证明,依靠单一的深度学习算法可以解决许多不同的任务,之前不同任务的研究都是独立分开研究算法的
事实上,真实的神经元计算着与RELU非常不同的函数,但更解决真实神经网络的系统并没有导致机器性能的提高
不应该认为深度学习在尝试模拟大脑,深度学习从许多领域获取灵感,特别是数学方面的研究
- 深度学习领域主要关注如何构建级计算机系统,从而成功解决需要智能才能解决的任务
- 计算神经科学领域主要关注构建大脑如何真实工作的、比较精确的模型
联结主义:当网络将大量简单的计算单元连接在一起时可以实现智能行为,期间有两个主要成就
- 分布式表示:每个神经元学习一个特征
- 反向传播、LSTM(1997)
与日俱增的数据量:
人工神经网络的第一个实验你在20世纪50年代就完成了,但直到现在才被认为是关键技术,一个粗略的经验法则:监督深度学习算法在每类给定约5000个标注样本情况下一般将达到可以接受的性能,当至少有1000万个标注样本的数据集用于训练时,它将达到或超过人类表现。同时我们也要关注如何通过无监督或半监督学习充分利用大量的未标注样本。
与日俱增的模型规模:
我们现在拥有的计算资源可以运行更大的模型。人工神经网络的规模大约每2.4年扩大一倍。这种增长是由更大内存、更快的计算机和更大的可用数据集驱动的。更大的网络能够在更复杂的任务重实现更高的精度。这种趋势看起来要持续十年。除非有能力扩展新技术,否则需要到21世纪50年代人工神经网络才能具备与人脑相同数量级的神经元。而且生物神经元表示的功能还更加复杂。GoogleNet其实比相对原始的额脊椎动物(青蛙)的神经系统还要小。【可是动物是要做很多项任务的,现在设计的神经网络基本就只是针对某项任务,真的有必要再再扩大吗,Time will tell】
第2章 线性代数
张量
一个数字是标量,一维数组是矢量,二维方阵称为二阶张量,把3维方阵称为三阶张量
第3章 概率与信息论
KL散度(Kullback-Leibler divergence)
如果对于同一个随机变量x有两个单独的概率分布P(x)和Q(x),可以使用KL散度来衡量着两个分布的差异:
$D_{KL}(P||Q)=E_{xsim P}[logfrac{P(x)}{Q(x)}]=E_{xsim P}[logP(x)-logQ(x)]$
$D_{KL}(P||Q) eq D_{KL}(Q||P)$
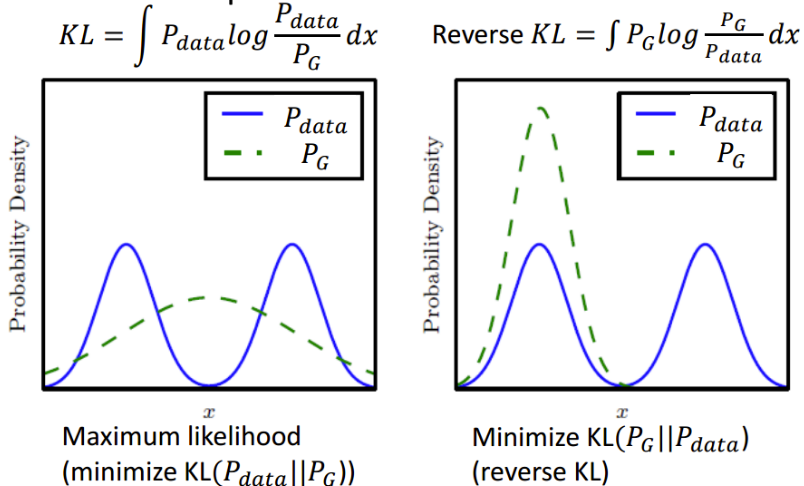
这种非对称性意味着选择$D_{KL}(P||Q)$还是$D_{KL}(Q||P)$影响很大
一个与KL散度密切联系的量是交叉熵$H(P,Q)=H(P)+D_{KL}(P||Q)$
第4章 数值计算
4.1 上溢和下溢
连续数学在数字计算机上的根本困难是,我们需要通过有限数量的位模式来表示无限多的实数,所以会引入舍入误差
下溢:当接近零的数字被四舍五入为零时会发生下溢
上溢:当大量级的数被近似为无穷大时发生上溢,返回非数字NaN
可以简单地依赖保证数值稳定的底层库
4.2 病态条件
条件数指的是函数相对于输入的微小变化而变化的快慢程度。
$f(x)=A^{-1}x$,当A具有特征值分解时,其条件数为$max|lamda_{i}/lamda_{j}|$,这是最大和最小特征值的模之比。当该数很大时,矩阵求逆对输入的误差特别敏感。
这种敏感性是矩阵本身的固有特性,而不是矩阵求逆期间舍入误差的结果。即使乘以完全正确的矩阵逆,病态条件的句子也会放大预先存在的误差。
4.3 基于梯度的优化方法
最速下降建议新的点为:
$x' = x - lr * abla_{x}f(x)$ lr是学习率,也就是步长
Jacobian矩阵:有时需要计算输入和输出都为向量的函数的所有偏导数。包含所有这样的偏导数的矩阵被称为Jacobian矩阵$J_{i,j}=frac{partial}{partial x_j}f(x)_i$
Hessian矩阵:当我们的函数具有多维输入时,二阶导数也有很多。我们可以将这些导数合并成一个矩阵,称为Hessian矩阵
$H(f)(x)_{i,j}=frac{partial^2}{partial x_i partial x_j}f(x)$ 分母处的对xi和xj的偏导顺序可以调换,所以Hessian矩阵是对称矩阵
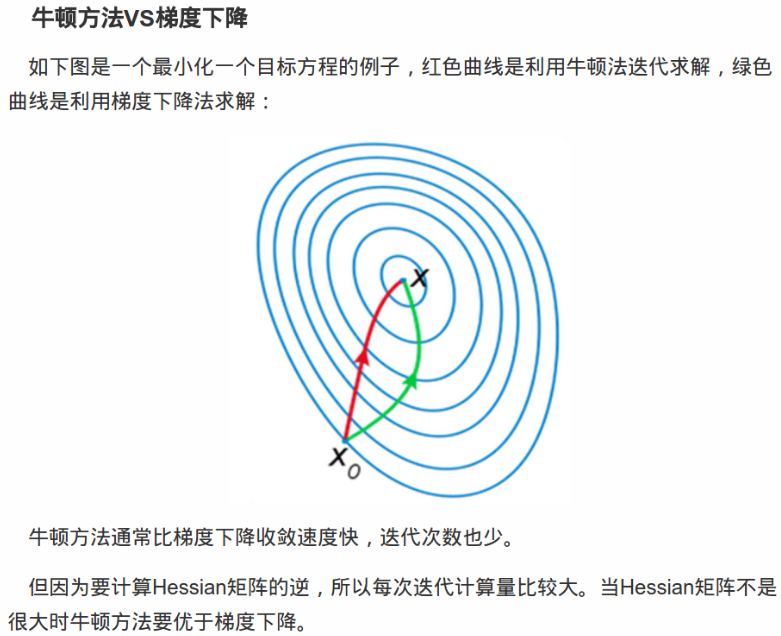
梯度下降无法利用包含在Hessian矩阵中的曲率信息。比如这里使用梯度下降来最小化Hessian矩阵条件数为5的二次函数f(x).这意味着最大曲率方向具有比最小曲率多5倍的曲率。
梯度下降会反复地在最大曲率(最陡峭)的方向下降,如果利用上Hessian矩阵的信息,与指向该方向的特征向量对应的Hessian的大的正特征值表示该方向上的导数快速增加,因此基于Hessian的优化算法可以预测,在此情况下最陡峭的方向实际不是最有前途的搜索方向。
仅适用梯度信息的优化算法称为一阶优化算法,如梯度下降;适用Hessian矩阵的优化算法称为二阶最优化算法,如牛顿法。
解释:
深度学习中使用的函数族是相当复杂的,所有深度学习算法往往缺乏理论保证。使用的优化函数也没有理论支持。
最成功的特定优化领域是凸优化。凸优化算法只对凸函数适用,即Hessian处处半正定的函数。因为这些函数没有鞍点而且所有全局极小值都是全局最小值点。但是深度学习中的大多数问题都难以表示成凸优化的形式。
4.4 约束优化
使用KKT方法解决,构建拉格朗日函数
第5章 机器学习基础
5.1 学习算法
机器学习算法是一种能够从数据中学习的算法。“学习”简洁的定义:对于某类任务T和性能度量P,一个计算机程序被认为可以从经验E中学习是指,通过经验E中学习是指,通过经验E改进后,它在任务T上由性能度量P衡量的性能有所提升。
性能度量P:准确率等,需要针对任务具体设计
经验E: 无监督学习算法 vs 监督学习算法 无监督学习算法训练含有很多特征的数据集,然后学习出这个数据集上有用的结果性质。比如学习生成数据集的整个概率分布,聚类
无监督学习和监督学习不是严格定义的术语,只是帮助我们粗略地划分研究的任务。无监督学习学习的联合概率可以通过链式法则进行分解,将其拆分成n个监督学习的问题,另外,求解监督学习问题p(y|x)时,也可以使用传统的无监督学习策略学习联合概率p(x,y),然后用贝叶斯公式进行推断
5.2 容量、过拟合和欠拟合
在先前未观测到的输入上表现良好的能力被称为泛化
通常是在训练集上最小化训练误差来训练模型,但是我们真正关注的是测试误差
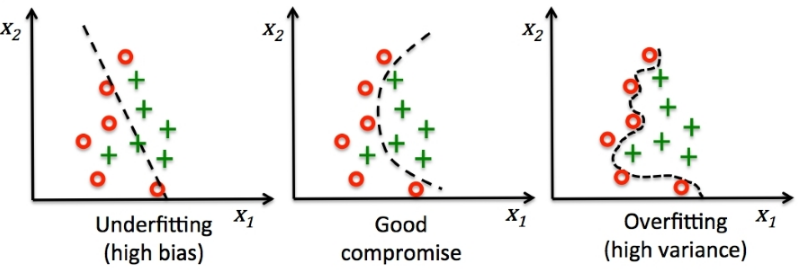
欠拟合:模型不能在训练集上获得足够低的误差(underfitting)
过拟合: 训练误差和测试误差之间的差距太大(overfitting)
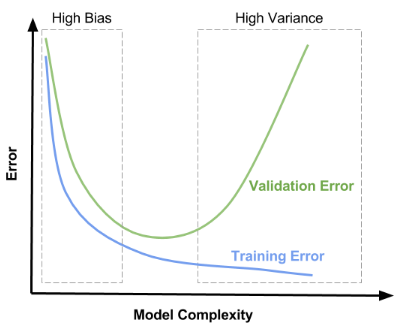
通过调整模型的容量(capacity),我们可以控制模型是否偏向于过拟合或者欠拟合。通俗来讲,模型的容量是指其拟合各种函数的能力。容量低的模型可能很难拟合训练集。容量高的模型可能会过拟合,因为记住了不适用于测试集的训练集性质。
一种控制训练算法容量的方法时选择假设空间(hypothesis space)(线性函数还是高次函数),即学习算法可以选择为解决方案的函数集
当机器学习算法的容量适合于所执行任务的复杂度和所提供训练数据的数量时,算法效果通常会最佳
奥卡姆剃刀:
在同样能够解释已知观测现象的假设中,我们应该挑选“最简单”的那一个(VC维理论支持)
统计学习理论提供了量化模型容量的不同方法。其中最有名的是VC维,VC维衡量的是二分类器的容量,VC维定义为该分类器能够分类的训练样本的最大数目。
统计学习中有个重要的结论:
- 训练误差和泛化误差之间的差异的上界随着模型容量增长而增长
- 但随着训练样本的增多而下降
泛化误差还与训练样本的数量有关
但是不适用于深度学习算法,因为深度学习算法的容量很难确定
模型的有效容量受限于优化算法的能力,确定深度学习模型容量的问题特别困难。
没有免费午餐定理(no free lunch theorem)
在所有可能的数据生成分布上平均之后,每一个分类算法在未事先观测的点上都有相同的错误率,换言之,没有一个机器学习算法总是比其他的要好。我们能够设想的最先进的算法和简单地将所有点归为同一类的简单算法有着相同的平均性能(在所有可能的任务上)
这意味着机器学习研究的目标不是找一个通用学习算法或是绝对最好的学习算法,只是期望学到在我们关注的数据生成分布上效果最好的算法
正则化
没有免费午餐定理暗示我们必须在特定任务上设计性能良好的机器学习算法,算法效果不仅很大程度上受影响与假设空间的函数数量,也取决于这些函数的具体形式。
权重衰减(weight decay): 对选择函数的一个偏好,设置的权重衰减系数乘以正则化项作为损失函数的额外惩罚
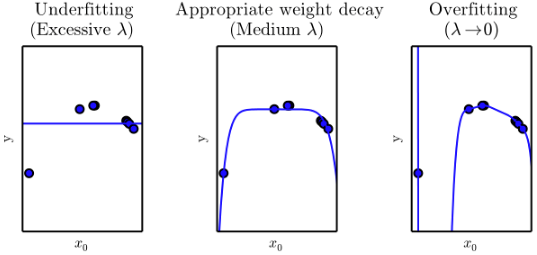
正则化是指修改学习算法,使其降低泛化误差而非训练误差,只有优化能够与正则化的重要性相提并论
超参数与验证集
用验证集来调超参数,通常80%的训练书用于训练,20%的用于验证
交叉验证:一个小规模的测试集意味着平均测试误差估计的统计不确定性,所以说交叉验证多用于小规模数据集,大规模数据集可以不用,太耗时了
最常见的方法时k折交叉验证:将数据集分成k个不重合的子集,测试误差可以估计为k次计算后的平均测试误差,在第i次测试时,数据的第i个子集用于测试集,其他的数据用于训练集