论文分享第三期-2019.03.29
Fully convolutional networks for semantic segmentation,CVPR 2015,FCN
一、全连接层与全局平均池化
在介绍FCN网络的全卷积连接之前,先介绍一下全连接层(fully connected layers)和全局平均池化(global average pooling)

以上两种实现GAP的方法,好像在程序中都有见过,也不太清楚那种更加合理,欢迎各位讨论指正。第二种方法中,卷积后面接激活函数;
二、FCN网络
优点:输入图像的尺寸任意,输出是与输入相同尺寸的语义分割图,即是像素级别的分类图。将浅层特征图谱和深层特征图谱反卷积的结果融合,再进行反卷积,使获得的结果兼具鲁棒性和细节。较浅层的结果更精细,较深层的结果更鲁棒。
缺点:仅借助卷积操作,考虑的图像中空间信息是局部的、不全面的。可以借助条件随机场CRF、非局部均值NML等方法改进。生成的结果细节表现能力有待提升。FCN是第一个端到端训练的、进行像素预测(语义分割)的全卷积网络。
FCN程序1-Marivn Teicha'mann/tensorflow-fcn,程序2-shelamer/fcn.berkeleyvision.org。本博文结合程序1,研究论文。
FCN-8算法框图:

框图中的模块说明:浅黄色的框和箭头表示卷积操作,正黄色的箭头表示反卷积操作,浅紫色的框表示最大池化,圆圈加号表示对应通道逐像素求和。紫红色的框为卷积操作得到的特征图,并非全连接层得到。
FCN-8模型,当输入图像为224x224x3时:
- 经过五组卷积和池化操作之后得到7x7x512大小的特征图谱,
- 然后用卷积操作代替传统的全连接层,第一个使用7x7的卷积核得到一个1x1x4096的特征图谱,第二个使用1x1的卷积核得到一个1x1x4096的特征图谱。
- 接下来为了得到像素级别的分类(语义分割),以VOC2007数据集为例,算上背景共有21类,所以将1x1x4096的特征图谱用1x1的卷积核得到一个1x1x21的类别图谱(程序中用score_fr表示),也就是一幅224x224大小的图像经过一系列的卷积操作后在21个各类别的概率得分,
- 然后进行反卷积得到整幅图像各像素点在21个各类别的概率得分。需要经过三次反卷积操作(正黄色的箭头),第一次1x1x21的类别图谱经过4x4、步长为2的卷积核,得到14x14x21的类别图谱(程序中用upscore表示),然后将pool-4输出的14x14x512特征图谱经过1x1、步长为1的卷积,得到14x14x21的类别图谱,最后再将两个类别图谱依通道逐像素求和,得到了融合浅层卷积特征的14x14x21的类别图谱。第二次与第一次反卷积的操作流程相同,最后得到的是28x28x21的类别图谱;第三次反卷积没有在融合更浅层的特征了,将28x28x21的类别图谱经过16x16、步长为8的卷积核,得到224x224x21的类别图谱,尺寸与输入的图像相同,
- 最后再转换为热力图可视化显示。
对于FCN-16,反卷积操作有两次,第一次使用4x4、步长为2的卷积核,第二次使用32x32、步长为16的卷积核。对于FCN-32,反卷积操作有一次,使用64x64、步长为32的卷积核(没有融合浅层的特征)。
FCN的一大特点就是允许任意尺寸的输入图像,对于不同尺寸的输入图像,所使用的操作都是上述框图中的,区别在于特征图谱的尺寸。如下图所示为全卷积网络,
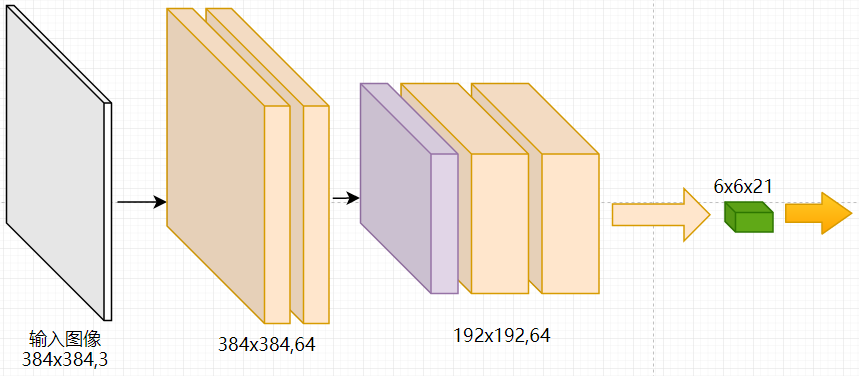
当输入为384×384的图像时:
- 经过五组卷积和池化操作后,pool-5的输出为12x12x512,
- 然后使用两个卷积核分别为7x7和1x1的全卷积操作,得到的输出为6x6x4096(输入尺寸=卷积核大小+步长x(输出尺寸-1)),
- 再使用1x1的卷积核得到6x6x21的类别图谱。
- 接下来就是框图中的三次反卷积操作,最终得到384x384x21的类别图谱,
以上的反卷积层因为是于pool-4和pool-3的尺寸对应,因此不受输入尺寸的影响。对比使用全连接层时的操作,因为需要将pool-5的特征图谱reshape成一条特征向量,对于224的输入,特征向量维度为7x7x512,则全连接层的权值尺寸为(7x7x512,4096);对于384的输入,特征向量维度为12x12x512,则全连接层的权值尺寸为(12x21x512,4096),全连接层的权值尺寸发生变化而不能训练。
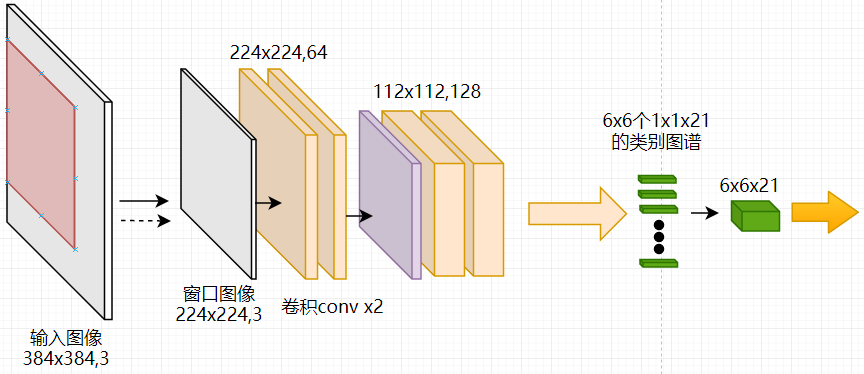
如下图为带有全连接层的网络,对于384的输入图像,当使用224×224尺寸的窗口、步长为32在384×384的图片上滑动,可以得到6x6个224x224的输入图像送给带全连接层的网络,然后得到6x6x21的类别图谱,与直接使用全卷积网络是相同的,但是使用全卷积网络效率更高。
三、Tensorflow中卷积与反卷积
卷积:tf.nn.conv2d(x, W, strides, padding=" ")
卷积核:W=[k, k, input_channel, output_channel]
反卷积:tf.nn.conv2d_transpose(x, W, output_shape, strides, padding=" ")
卷积核:W=[k, k, output_channel, input_channel]
输出尺寸:output_shape=[out_feature_h, out_feature_w, output_channel],out_feature_h、w为指定的输出尺寸