给定一个二叉树,确定它是否是一个完全二叉树。
百度百科中对完全二叉树的定义如下:
若设二叉树的深度为 h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。(注:第 h 层可能包含 1~ 2h 个节点。)
示例 1:
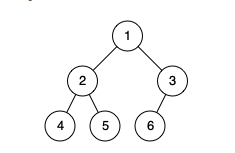
输入:[1,2,3,4,5,6] 输出:true 解释:最后一层前的每一层都是满的(即,结点值为 {1} 和 {2,3} 的两层),且最后一层中的所有结点({4,5,6})都尽可能地向左。
示例 2:

输入:[1,2,3,4,5,null,7] 输出:false 解释:值为 7 的结点没有尽可能靠向左侧。
提示:
- 树中将会有 1 到 100 个结点。
个人递归方法:
class Solution {
bool isTheEnd = false;
int depth = 0;
public:
bool isCompleteTree(TreeNode* root)
{
if (root == NULL)
return true;
depth = GetDepth(root);
return GetAns(root, 1);
}
int GetDepth(TreeNode *root)
{
if (root == NULL)
return 0;
return max(GetDepth(root->left), GetDepth(root->right)) + 1;
}
bool GetAns(TreeNode *root, int dep)
{
//只有根节点的情况,不用判空,因为不会递归到那
if (dep == depth)
{
return true;
}
if (dep < depth - 1)
{
if (root->left == NULL || root->right == NULL)
return false;
return GetAns(root->left, dep + 1) && GetAns(root->right, dep + 1);
}
else if (dep == depth - 1)
{
if (isTheEnd)
{
if (root->left != NULL || root->right != NULL)
return false;
return true;
}
else
{
if (root->left == NULL)
{
if (root->right != NULL)
return false;
isTheEnd = true;
return true;
}
if (root->right == NULL)
{
isTheEnd = true;
return true;
}
return true;
}
}
}
};广度优先遍历法(推荐):
bool isCompleteTree(TreeNode* root) {
queue<TreeNode *> que;
que.push(root);
while(!que.empty())
{
TreeNode * node = que.front();
que.pop();
if(!node)
{
break;
}
else
{
que.push(node->left);
que.push(node->right);
}
}
while(!que.empty())
{
TreeNode * node=que.front();
if(node)
return false;
que.pop();
}
return true;
}