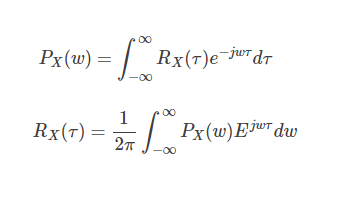首先,概念解释:
自相关函数R(t1,t2):为了衡量随机过程x(t)在任意两个时刻(t1,t2)上获得的随机变量之间的关联程度。
R(t1,t2) = E[ x(t1) x(t2) ] 或者写成 R(τ) = E[ x(t) x(t+τ) ] 互相关函数:是描述随机信号x(t),y(t)在任意两个不同时刻t1,t2的取值之间的相关程度。:是描述随机信号x(t),y(t)在任意两个不同时刻t1,t2的取值之间的相关程度。R(t1,t2) = E[ x(t1) y(t2) ] 平稳随机过程:是一类应用非常广泛的随机过程,统计特性和时间起点无关。均值与t无关,为常数a;自相关函数只和时间间隔
τ有关, R(t1,t1+τ) =R(τ) 。平稳过程的功率谱密度与其自相关函数是一对傅里叶变化(Winner-Khintchine定理)在信号处理领域,自相关和互相关函数的定义如下:
设原函数是f(t),则自相关函数定义为R(u)=f(t)*f(-t),其中*表示卷积;
设两个函数分别是f(t)和g(t),则互相关函数定义为R(u)=f(t)*g(-t),它反映的是两个函数在不同的相对位置上互相匹配的程度。
从数学的角度来讲,相关是一个与卷积类似的运算.相关是指将一个函数滑过另一个函数并求出两者乘积下的面积.在卷积的运算中,其中一个函数要针对纵轴做翻转,然后再求两函数滑动相乘的面积和.而相关运算中,两个函数不做任何翻转直接进行相对滑动的乘积面积和.
进而,两个相同函数的相关运算称为自相关.而两个不相同的函数的相关运算称为互相关.
那么,其实从定义中我们很好理解.一般来讲,自相关函数得到的自相关运算是比较大的.因为两个相同的信号相互滑过,相乘的面积肯定是很大的.但当两个函数的相关性为0的时候,两个函数就不会有重合的情况,在时域上来讲就不可能存在相似的情况
通过这个解释,让我更好的理解了“相关”的概念。