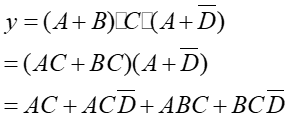1 、常见的简称:
FPGA :现场可编程门阵列,Field-Programmable Gate Array
PLD :可编程逻辑器件,programmable logic device
ASIC :专用集成电路,Application Specific Integrated Circuit
LUT :查找表,Look-Up-Table
CLB :可配置逻辑块,Configurable Logic Block
2、可编程逻辑器件PLD
可编程逻辑器件(PLD)是厂家作为一种通用型器件生产的半定制电路,用户利用软件和硬件开发工具对器件进行设计和编程,通过配置、更改器件内部逻辑单元和连接结构,从而实现所需要的逻辑功能。
2.1 PLD优点:
可编程逻辑器件(CPLD)可在任何时间改变,从而完成许多种不同的功能。设计人员可利用价格低廉的软件工具快速开发、仿真和测试其设计。 然后,可快速将设计编程到器件中,并立即在实际运行的电路中对设计进行测试。另一个关键优点是在设计阶段中客户可根据需要修改电路,直到对设计工作感到满意为止。 这是因为PLD基于可重写的存储器技术--要改变设计,只需要简单地对器件进行重新编程。 一旦设计完成,客户可立即投入生产,只需要利用最终软件设计文件简单地编程所需要数量的PLD就可以了。
2.2 PLD主要类型
可编程逻辑器件的两种主要类型是:现场可编程门阵列(FPGA)和复杂可编程逻辑器件(PLD)。
在这两类可编程逻辑器件中,FPGA提供了最高的逻辑密度、最丰富的特性和最高的性能。 现在最新的FPGA器件,如Xilinx Virtex系列中的部分器件,可提供八百万"系统门"(相对逻辑密度)。 这些先进的器件还提供诸如内建的硬连线处理器(如IBM Power PC)、大容量存储器、时钟管理系统等特性,并支持多种最新的超快速器件至器件(device-to-device)信号技术。 FPGA被应用于范围广泛的应用中,从数据处理和存储,以及到仪器仪表、电信和数字信号处理等。
PLD有可编程只读存储器(PROM)、可擦除可编程存储器(EPROM)、可编程逻辑阵列(简称PLA)、可编阵列逻辑(简称PAL)和通用阵列逻辑(简称GAL)等几种。

(按器件集成度的粗暴划分方法)
2.2.1 按器件结构类型划分:
(1):乘积项结构器件。其基本结构为“与-或阵列”的器件。简单PLD、EPLD及CPLD都属于此类器件
(2):查找表结构器件。其基本结构类似于“门阵列”的器件,它由简单的查找表组成可编程逻辑门,再构成阵列形式。大多数FPGA都属于此类器件。
2.2.2 根据其掉电后重新上电能否保持变成信息划分
(1):CPLD。掉电后重新上电还能持编程信息的器件。
(2):FPGA。掉电后不能保持编程信息的器件。
3 、FPGA基本知识
目前,主流FPGA都采用基于SRAM工艺的查找表结构。由存放在片内RAM 中的程序来设置其工作状态的,因此,工作时需要对片内的RAM 进行编程。用户可以根据不同的配置模式,采用不同的编程方式。
需要在使用时外接一个片外存储器以保存程序。上电后,FPGA把外部存储器中的数据读入片内RAM,完成配置后,进入工作状态;掉电后,FPGA的内部逻辑消失。
因此,FPGA 能够反复使用。FPGA 的编程无须专用的FPGA 编程器,只须用通用的EPROM、PROM 编程器即可。这样,同一片FPGA,不同的编程数据,可以产生不同的电路功能。因此,FPGA 的使用非常灵活。
3.1 查找表
LUT本质就是一个RAM,常见的是4输入或者6输入。可看成一下有4(或6)位地址线的16x1(或64x1)的RAM。用户通过HLD语言描述一个逻辑电路,FPGA开发软件计算后把真值表写进RAM。相当于一个N选1的数据选择器。
这样对输入信号进行逻辑运算就相当于输入一个地址进行查表,找出并输出地址对应的内容。如果把输出的D触发器旁路而直接输出,则便实现了组合逻辑,反之,如果有D触发器则实现了时序逻辑。
3.2 结构
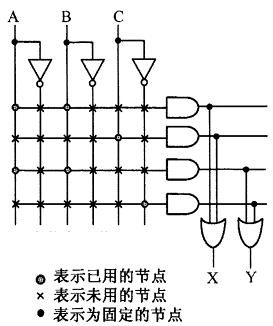
(1)乘积项结构
左图就是所谓的乘积项结构,它实际上就是一个与或结构。可编程交叉点一旦导通,则实现了“与”逻辑,后面带有一个固定编程的“或”逻辑,这样就形成了一个组合逻辑。
右图实现了