1 注意空指针,
2 空类型,没有任何成员变量和成员函数,对改类型求sizeof
结果为1,本来应该是0,但当我们声明该实例的时候,他必须在内存种占有一点空间,否则无法使用该实例。
(1)加上构造函数和析构函数
还是1
(2)弄个虚析构函数
多了指向虚函数表的指针。32位上,一个指针4字节,所以为4。 64位上,一个指针8字节,所以为8。
3 复制构造函数的参数要用常量引用 const & 不然会永无休止的递归调用
4 赋值运算符函数
(1)是否把返回值的类型声明为该类型的引用。
(2)是否把传入的参数的类型声明为常量引用。(不然有无所谓的开销)
(3)是否释放了原本实例自身的内存。(避免内存泄漏)
(4)是否判断传入的参数和当前的实例是同一个实例。
5 sizeof 数组 是数组的大小(编译期就能确定的) sizeof 指针是 指针的大小。区分好指针和数组。
6 二维数组中的查找
每一行都按照从左到右递增。每一列都从上到下递增。输入这样一个二维数组,和一个数,判断这个数是否存在于这个数组。
从右上角开始比大小,大于剔除该行,小于剔除该列。
7 字符串
char s1[]="123456"; char s2[]="123456"; char*s3="123456"; char*s4="123456";
s1!=s2 s3==s4 &s3!=&s4
8 替换空格
把字符串的空格替换成三个字符%20。
先遍历一次,有多少个空格。然后分配好内存。从后往前复制。
9 从尾到头打印链表
(1)能否反转指针。(改变了结构)
(2)用栈来实现。
10 重建二叉树

要求里面的值是不同的。
11 用两个栈实现队列。

12 用两个队列实现栈

13 旋转数组的最小数字
实际是两个排序的子数组。,前面的大于后面的。用首尾中,二分法。
14 斐波那契数列
从下往上算。
(1)一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶,求该青蛙跳上一个n级台阶总共有多少种跳法
f(n)=f(n-1)+f(n-2)
15 二进制中1的个数。
(1)flag=1,不断 <<1,&。
(2)n&(n-1);会去掉最低位的1。不断while 直到n=0
16 数值的整数次方。
实现pow 出错返回什么,0的0次方为0 或1 底数double 是否为0 不能用!= 要<=0.0000001。注意底数可以为负。
17 打印1到最大的n位数
注意溢出,使用字符串来打印数字 (使用递归) 注意0开头。
18 在o(1)时间删除链表节点
给定单向链表的头指针和一个删除节点指针。
(1)遍历,找到删除节点的上一个指针。
(2)把删除节点next节点的内容覆盖到删除节点,然后删除节点指向next next 。小心删除节点为尾节点(此时只能遍历了)
19 调整数组顺序使奇数位于偶数前面
(1)类似快排的方法,一个指针从前向后停在偶数,第二个指针从后向前停在奇数。
(2)把判断方法抽象出来,变为一个函数。
20 链表中倒数第k个节点
(1)两个指针,一个在另一个的前k个节点,小心链表大小小于k
21 二叉树的镜像
输入一个二叉树,该函数输出它的镜像
递归交换左右子树就行
22 包含min函数的栈
得到栈的最小元素的min函数,调用min push pop的时间复杂度都是o(1)
弄多个min栈,用来存原始栈的最小值,pop同时pop push的话判断push的值跟min栈的pop谁大。
23 栈的压入、弹出序列。
给一个压入顺序判断第二个序列是否该栈的弹出顺序。
直接模拟就行。
24 从上往下打印二叉树
使用队列,push进节点。如果pop的值有子节点则该子节点push进去。
25 二叉搜索树的后续遍历序列
输入一个整数数组,判断该数组是不是某二叉搜索树的后续遍历的结果。,假设输入的数组的任意两个数字都不相同。
最后一个值是根,然后数组中连续的比根值小的数是左子树,大的是右子树。递归判断是否存在违背的情况。
26 二叉树中和为某一值的路径。
前序遍历
27 复杂链表的复制
复杂链表中,每个节点除了有一个next指针指向下一个节点外,还有一个sibling指向链表中的任意节点或者NULL。
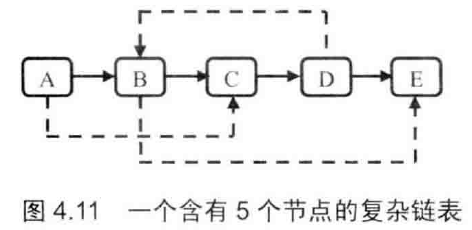

(1)两步,第一步弄好next 第二步弄好 sibling 复杂度 n^2 主要消耗是在定位sibling上。
(2)空间换时间,用哈希表绑定 原节点和副本节点。节省查找sibling的时间
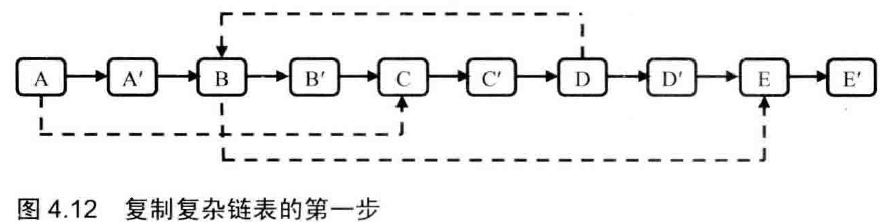
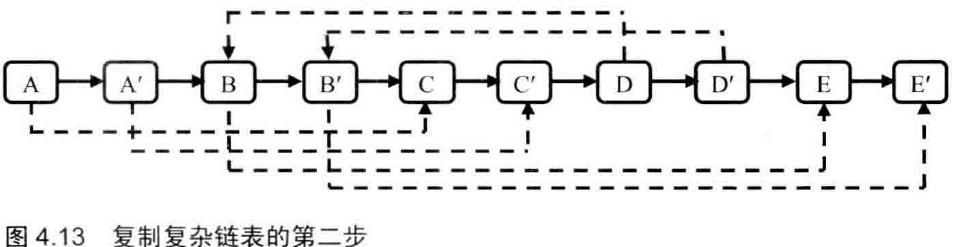
(3)直接复制在原链表后面,且把sibling连好后,再拆开
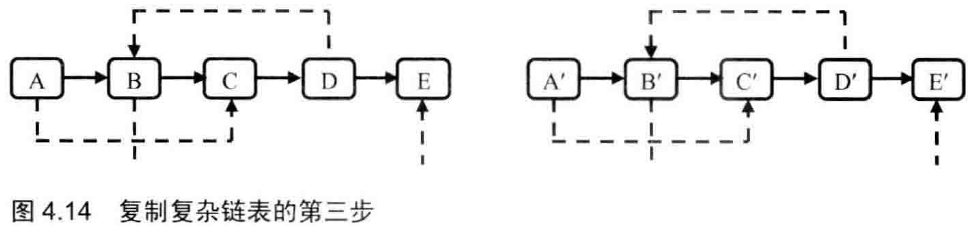
28 二叉搜索树与双向链表
递归的去获得左子树最右和右子树最左 并返回自身的最右
29 字符串的排列
输入abc,输出a b c所能排列出来的所有字符串abc,acb,bac,bca,cab,cba
固定一个,然后把这一个逐个和后面的字符交换。n++;继续 递归

29 数组中出现次数超过一半的数字
(1)partition函数求中位数 o(n)
(2)遍历时保存一个值以及次数,当遍历值相同时,次数加1 不同时,次数减1。次数为0则选择下一个遍历的数字。
30 最小的k个数
(1)partition函数
(2)最大堆
31 从1到n整数中1出现的次数
(1)例如21346 把这个数分成 从1到1345,1346到21345 分析
10000到19999第5位为1出现的次数时10000次
32 把数组排成最小的数例如{3 32 321} 排成321323
(1)把数组排序就行。排序方法 两个数字 m n。mn<nm则 m应该再n前面。
33 第一个只出现一次的字母
hash到一个26数组原本为0,存 第一次位置,若非0则置-1。遍历完后查找最小的正数对应的字母。
34 两个链表的第一个公共节点
(1)栈,把两个链表各自压进栈中,然后pop直到最后一个相同的节点。
(2)比较长度,如一个为 9 一个为7 则9的那个先走2步。
35 数字在排序数组中出现的次数
(1)最基本的遍历为o(n) 利用二分 o(logn)
36 树的深度
(1)递归 左子树右子树是根的深度+1。从上往下。
37 判断树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1,那么它就是一颗平衡二叉树。
(1)后续遍历,得到他的根之前就已经得到左右子树的高度,就能递归向上判断是不是平衡的。根为深度大的那个子树+1。
38 数组中只出现一次的数字。
一个整形数组里除了两个数字之外,其他的数字都出现了两次。找出这两个只出现一次的数字。时间复杂度是o(n) 空间复杂度o(1)
把所有元素都遍历异或一遍,异或值肯定有一个位不为0,按这个位是否为0区分开两组(把那两个单独的数字分开了),然后继续组内异或,得到的值就是出现一次的数。
39 和为s的两个数字
数组排序,把第一个跟最后一个进行匹配。然后前进。
40 字符串二次旋转
41 n个骰子的点数
用两个数组来存骰子点数的每一个总数出现的次数,一次循环中,第一个数组中的第n个数字表示骰子和为n出现的次数。在下一循环中,我们加上一个新骰子,此时和为n的骰子出现的次数应该等于上衣循环中的骰子点数 n-1 n-2 n-3 n-4 n-5 n-6之和。
42 求1+2+3+n
(1)利用构造函数求解 static int n,sum;每次++n sum+=n;
43 树中两个节点的最低公共祖先
(1)二叉搜索树 找到在两个输入值的中间值。
(2)有父指针的普通树 弄成两个链表求公共节点。
(3) 无父指针的普通树 遍历弄成一个栈来找节点
44 数字中重复的数字
len(a)!=len(set(a))。即把相应的值移到相应的位置
45 正则表达式匹配
写代码
46 表示数值的字符串
坑多,写代码
47 字符流中第一个不重复的字符
hash到一个26数组原本为0,存 第一次位置,若非0则置-1。遍历完后查找最小的正数对应的字母。
48 链表中环的入口节点
(1)快慢指针相遇时,肯定已经在环内。这个时候走一圈,就能知道环的大小。
(2)两个指针在头部,其中一个先走 环的大小步。他们相遇的地方就是入口节点。
49 删除链表中的重复节点
(1) 小心null 重复节点在尾部,重复节点在头部。
50 二叉树中序遍历的下一个节点
还有父指针。
(1)如果一个节点有右子树,那么下一个节点就是它右子树的最左子节点。
如果没有右子树,如果节点是它父节点的左子节点,那么下一个节点就是它的父节点。
如果节点是它父节点的右子节点,那么久沿着父指针向上遍历,直到找到一个是它父节点的左子节点的节点。如果存在那么该父节点就是下一个节点。不存在则为null
51 对称的二叉树
前序遍历 根左右 根右左 如果相同则对称
52 把二叉树打印成多行
队列
53 按之字形顺序打印二叉树
用两个栈来弄
54 序列化二叉树
null用特殊符号表示
55 二叉搜索树第k个节点
中序遍历
56 数据流中的中位数
同时使用最大堆,最小堆。保证两边的数据之差不超过1。
数据的总数目是偶数时,把新数据插入到最小堆。否则插入到最大堆。
保证最大堆中的所有数据都要小于最小堆中的数据。 如果偶数时插入到最小堆的数字比最大堆中的某些数据小,则把这个数据插入到最大堆中,然后把最大堆中的最大树插入到最小堆中。
57 滑动窗口的最大值
输入数组{2,3,4,2,6,2,5} 滑动窗口大小为3 那么一共6个滑动窗口,他们的最大值分别为{4,4,6,6,6,5}
也弄个队列,比当前值小的直接弄进去。因为可能当前窗口会滑动,比当前值大的直接替换掉当前值。