欧拉函数

处理何种问题：用于求解[1,n]中有多少个数与n互质的个数。

 

性能：单次查询时间复杂度为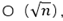，打表的话有一个线性筛，时间复杂度为O(n)。

 

原理：

可以先在1到n-1中找到与n不互质的数，然后把他们减掉

比如φ(12)

把12质因数分解，12=2*2*3，其实就是得到了2和3两个质因数

然后把2的倍数和3的倍数都删掉

2的倍数：2,4,6,8,10,12

3的倍数：3,6,9,12

本来想直接用12 - 12/2 - 12/3

但是6和12重复减了

所以还要把即是2的倍数又是3的倍数的数加回来 (＞﹏＜)

所以这样写12 - 12/2 - 12/3 + 12/(2*3)

这叫什么，这叫容斥啊，容斥定理听过吧

比如φ(30)，30 = 2*3*5

所以φ(30) = 30 - 30/2 - 30/3 - 30/5 + 30/(2*3) + 30/(2*5) + 30/(3*5) - 30/(2*3*5)

但是容斥写起来好麻烦(￣.￣)

有一种简单的方法

φ(12)   =   12*(1 - 1/2)*(1 - 1/3)                 =   12*(1 - 1/2 - 1/3 + 1/6)

φ(30)   =   30*(1 - 1/2)*(1 - 1/3)*(1 - 1/5)   =   30*(1 - 1/2 - 1/3 - 1/5 + 1/6 + 1/10 + 1/15 - 1/30)

你看( •̀∀•́ )，拆开后发现它帮你自动帮你容斥好

所以φ(30)的计算方法就是先找30的质因数

分别是2,3,5

然后用30* 1/2 * 2/3 * 4/5就搞定了

顺便一提，phi(1) = 1

摘自：https://www.cnblogs.com/linyujun/p/5194170.html#undefined

 

实现步骤：略，找的板子，来自上述网址

输入样例解释：

无

输出样例解释：

无

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string.h>
using namespace std;
///欧拉函数
long long PHI(long long x)
{
    long long ans = x;
    for(long long i = 2; i*i <= x; i++)
    {
        if(x % i == 0)
        {
            ans = ans / i * (i-1);
            while(x % i == 0)
                x /= i;
        }
    }
    if(x > 1)
        ans = ans / x * (x-1);
    return ans;
}
///欧拉表
const int N =20000010 ;
long long phi[N], prime[N];
long long tot;///tot计数，表示prime[N]中有多少质数
void Euler()
{
    phi[1] = 1;
    for(long long i = 2; i < N; i ++)
    {
        if(!phi[i])
        {
            phi[i] = i-1;
            prime[tot ++] = i;
        }
        for(long long j = 0; j < tot && i*prime[j] < N; j ++)
        {
            if(i % prime[j])
                phi[i * prime[j]] = phi[i] * (prime[j]-1);
            else
            {
                phi[i * prime[j] ] = phi[i] * prime[j];
                break;
            }
        }
    }
}

int main()
{
    Euler();
    for(int i=1; i<=20; ++i) ///前20欧拉数的表
    {
        printf("%d:%lld
",i,phi[i]);
    }
    return 0;
}
/**
1:1
2:1
3:2
4:2
5:4
6:2
7:6
8:4
9:6
10:4
11:10
12:4
13:12
14:6
15:8
16:8
17:16
18:6
19:18
20:8
*/