很多读者反应,就算看了前文 动态规划详解,了解了动态规划的套路,也不会写状态转移方程,没有思路,怎么办?本文就借助「最长递增子序列」来讲一种设计动态规划的通用技巧:数学归纳思想。
最长递增子序列(Longest Increasing Subsequence,简写 LIS)是比较经典的一个问题,比较容易想到的是动态规划解法,时间复杂度 O(N^2),我们借这个问题来由浅入深讲解如何写动态规划。
比较难想到的是利用二分查找,时间复杂度是 O(NlogN),我们通过一种简单的纸牌游戏来辅助理解这种巧妙的解法。
先看一下题目,很容易理解:

注意「子序列」和「子串」这两个名词的区别,子串一定是连续的,而子序列不一定是连续的。下面先来一步一步设计动态规划算法解决这个问题。
一、动态规划解法
动态规划的核心设计思想是数学归纳法。
相信大家对数学归纳法都不陌生,高中就学过,而且思路很简单。比如我们想证明一个数学结论,那么我们先假设这个结论在 k<n 时成立,然后想办法证明 k=n 的时候此结论也成立。如果能够证明出来,那么就说明这个结论对于 k 等于任何数都成立。
类似的,我们设计动态规划算法,不是需要一个 dp 数组吗?我们可以假设 d**p[0...i−1] 都已经被算出来了,然后问自己:怎么通过这些结果算出dp[i] ?
直接拿最长递增子序列这个问题举例你就明白了。不过,首先要定义清楚 dp 数组的含义,即 dp[i] 的值到底代表着什么?
我们的定义是这样的:****dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度。
举个例子:
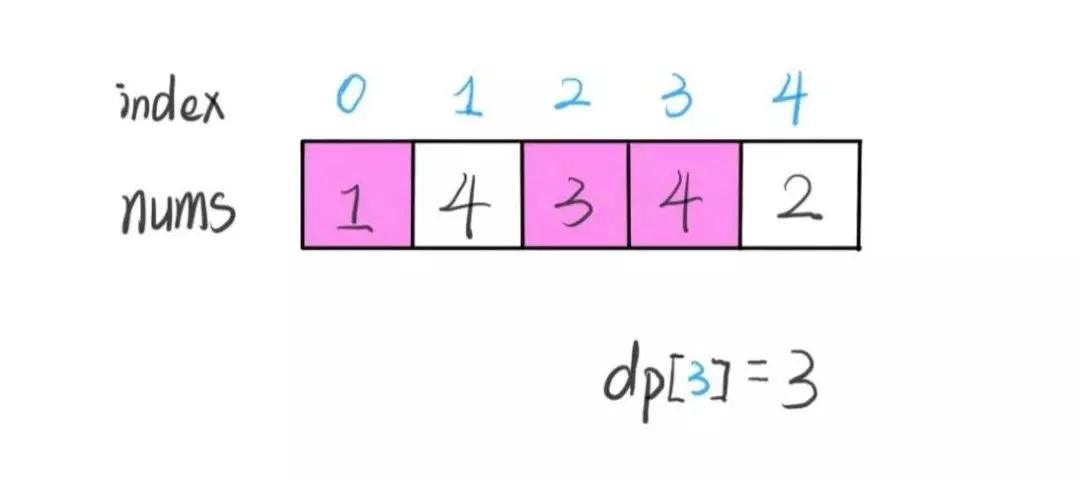
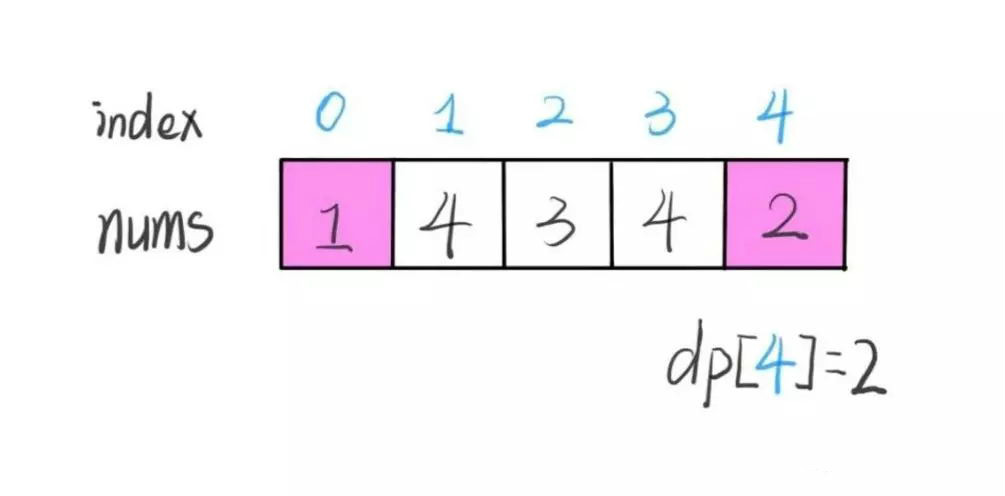
算法演进的过程是这样的:
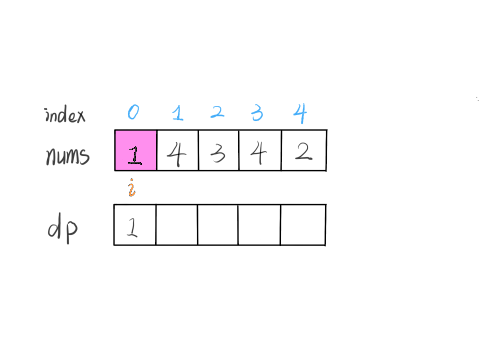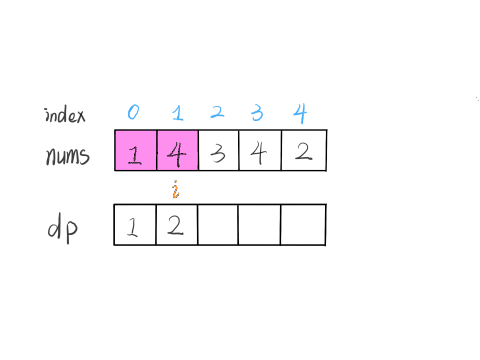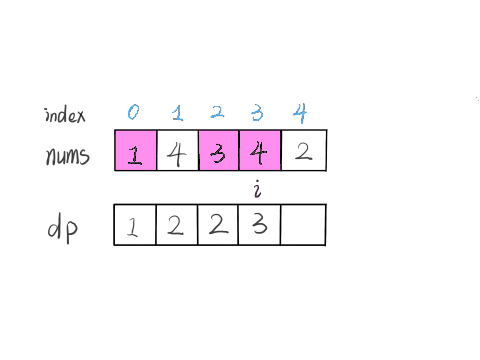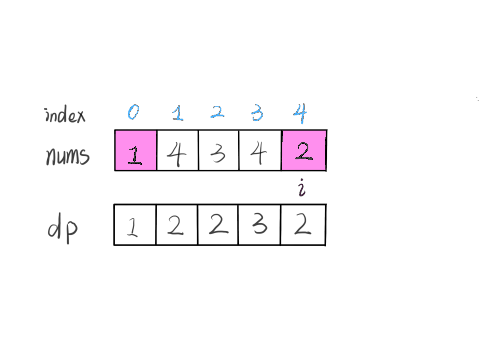
根据这个定义,我们的最终结果(子序列的最大长度)应该是 dp 数组中的最大值。
int res = 0;
for (int i = 0; i < dp.length; i++) {
res = Math.max(res, dp[i]);
}
return res;
读者也许会问,刚才这个过程中每个 dp[i] 的结果是我们肉眼看出来的,我们应该怎么设计算法逻辑来正确计算每个 dp[i] 呢?
这就是动态规划的重头戏了,要思考如何进行状态转移,这里就可以使用数学归纳的思想:
我们已经知道了 d**p[0...4] 的所有结果,我们如何通过这些已知结果推出 d**p[5]呢?
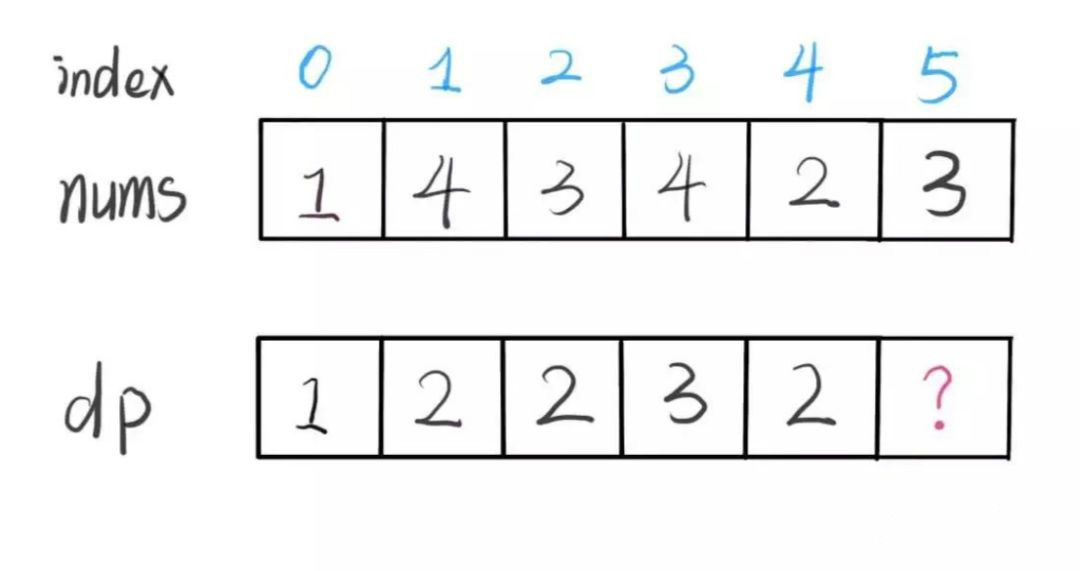
根据刚才我们对 dp 数组的定义,现在想求 dp[5] 的值,也就是想求以 nums[5] 为结尾的最长递增子序列。
nums[5] = 3,既然是递增子序列,我们只要找到前面那些结尾比 3 小的子序列,然后把 3 接到最后,就可以形成一个新的递增子序列,而且这个新的子序列长度加一。
当然,可能形成很多种新的子序列,但是我们只要最长的,把最长子序列的长度作为 dp[5] 的值即可。
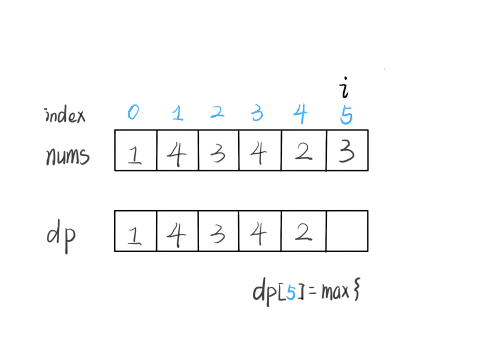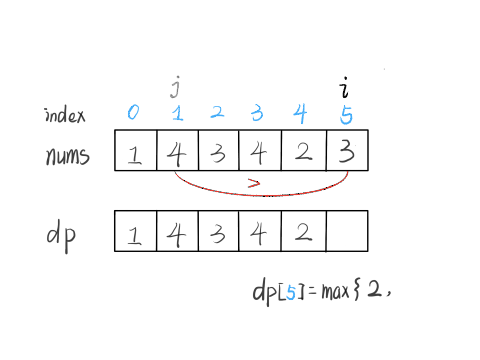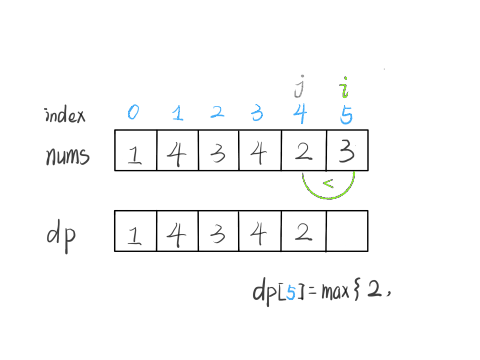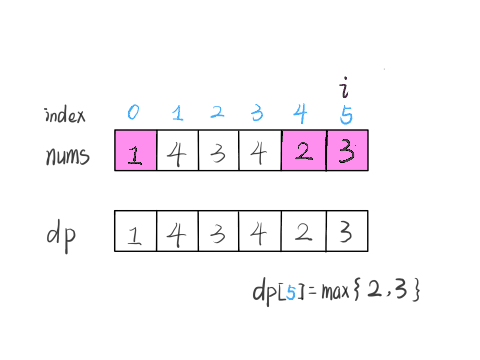
for (int j = 0; j < i; j++) {
if (nums[j] < nums[i])
dp[i] = Math.max(dp[i], dp[j] + 1);
}
这段代码的逻辑就可以算出 dp[5]。到这里,这道算法题我们就基本做完了。读者也许会问,我们刚才只是算了 dp[5] 呀,dp[4], dp[3] 这些怎么算呢?
类似数学归纳法,你已经可以通过 dp[0...4] 算出 dp[5] 了,那么任意 dp[i] 你肯定都可以算出来:
for (int i = 0; i < nums.length; i++) {
for (int j = 0; j < i; j++) {
if (nums[j] < nums[i])
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
还有一个细节问题,就是 base case。dp 数组应该全部初始化为 1,因为子序列最少也要包含自己,所以长度最小为 1。下面我们看一下完整代码:
public int lengthOfLIS(int[] nums) {
int[] dp = new int[nums.length];
// dp数组全部初始化为1
Arrays.fill(dp, 1);
for (int i = 0; i < nums.length; i++) {
for (int j = 0; j < i; j++) {
if (nums[j] < nums[i])
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
int res = 0;
for (int i = 0; i < dp.length; i++)
res = Math.max(res, dp[i]);
return res;
}
至此,这道题就解决了,时间复杂度 O(N^2)。总结一下动态规划的设计流程:
首先明确 dp 数组所存数据的含义。这步很重要,如果不得当或者不够清晰,会阻碍之后的步骤。
然后根据 dp 数组的定义,运用数学归纳法的思想,假设 d**p[0...i−1] 都已知,想办法求出 d**p[i],一旦这一步完成,整个题目基本就解决了。
但如果无法完成这一步,很可能就是 dp 数组的定义不够恰当,需要重新定义 dp 数组的含义;或者可能是 dp 数组存储的信息还不够,不足以推出下一步的答案,需要把 dp 数组扩大成二维数组甚至三维数组。