一、决策树分类算法概述
决策树算法是从数据的属性(或者特征)出发,以属性作为基础,划分不同的类。例如对于如下数据集

(数据集)
其中,第一列和第二列为属性(特征),最后一列为类别标签,1表示是,0表示否。决策树算法的思想是基于属性对数据分类,对于以上的数据我们可以得到以下的决策树模型

(决策树模型)
先是根据第一个属性将一部份数据区分开,再根据第二个属性将剩余的区分开。
实现决策树的算法有很多种,有ID3、C4.5和CART等算法。下面我们介绍ID3算法。
二、ID3算法的概述
ID3算法是由Quinlan首先提出的,该算法是以信息论为基础,以信息熵和信息增益为衡量标准,从而实现对数据的归纳分类。
首先,ID3算法需要解决的问题是如何选择特征作为划分数据集的标准。在ID3算法中,选择信息增益最大的属性作为当前的特征对数据集分类。信息增益的概念将在下面介绍,通过不断的选择特征对数据集不断划分;
其次,ID3算法需要解决的问题是如何判断划分的结束。分为两种情况,第一种为划分出来的类属于同一个类,如上图中的最左端的“非鱼类”,即为数据集中的第5行和第6行数据;最右边的“鱼类”,即为数据集中的第2行和第3行数据。第二种为已经没有属性可供再分了。此时就结束了。
通过迭代的方式,我们就可以得到这样的决策树模型。

(ID3算法基本流程)
三、划分数据的依据
ID3算法是以信息熵和信息增益作为衡量标准的分类算法。
1、信息熵(Entropy)
熵的概念主要是指信息的混乱程度,变量的不确定性越大,熵的值也就越大,熵的公式可以表示为:
其中,=frac{left&space;|&space;u_i&space;
ight&space;|}{left&space;|&space;S&space;
ight&space;|}) ,
,) 为类别
为类别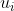 在样本
在样本 中出现的概率。
中出现的概率。
2、信息增益(Information gain)
信息增益指的是划分前后熵的变化,可以用下面的公式表示:
其中, 表示样本的属性,
表示样本的属性,) 是属性
是属性 所有的取值集合。
所有的取值集合。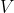 是
是 的其中一个属性值,
的其中一个属性值, 是
是 中
中 的值为
的值为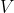 的样例集合。
的样例集合。
四、实验仿真
1、数据预处理
我们以下面的数据为例,来实现ID3算法:

摘自 http://blog.sina.com.cn/s/blog_6e85bf420100ohma.html
我们首先需要对数据处理,例如age属性,我们用0表示youth,1表示middle_aged,2表示senior等等。

(将表格数据化)
2、实验结果

(原始的数据)

(划分1)

(划分2)

(划分3)

(最终的决策树)
MATLAB代码
主程序

%% Decision Tree % ID3 %导入数据 %data = [1,1,1;1,1,1;1,0,0;0,1,0;0,1,0]; data = [0,2,0,0,0; 0,2,0,1,0; 1,2,0,0,1; 2,1,0,0,1; 2,0,1,0,1; 2,0,1,1,0; 1,0,1,1,1; 0,1,0,0,0; 0,0,1,0,1; 2,1,1,0,1; 0,1,1,1,1; 1,1,0,1,1; 1,2,1,0,1; 2,1,0,1,0]; % 生成决策树 createTree(data);

function [ output_args ] = createTree( data ) [m,n] = size(data); disp('original data:'); disp(data); classList = data(:,n); classOne = 1;%记录第一个类的个数 for i = 2:m if classList(i,:) == classList(1,:) classOne = classOne+1; end end % 类别全相同 if classOne == m disp('final data: '); disp(data); return; end % 特征全部用完 if n == 1 disp('final data: '); disp(data); return; end bestFeat = chooseBestFeature(data); disp(['bestFeat: ', num2str(bestFeat)]); featValues = unique(data(:,bestFeat)); numOfFeatValue = length(featValues); for i = 1:numOfFeatValue createTree(splitData(data, bestFeat, featValues(i,:))); disp('-------------------------'); end end

%% 选择信息增益最大的特征 function [ bestFeature ] = chooseBestFeature( data ) [m,n] = size(data);% 得到数据集的大小 % 统计特征的个数 numOfFeatures = n-1;%最后一列是类别 % 原始的熵 baseEntropy = calEntropy(data); bestInfoGain = 0;%初始化信息增益 bestFeature = 0;% 初始化最佳的特征位 % 挑选最佳的特征位 for j = 1:numOfFeatures featureTemp = unique(data(:,j)); numF = length(featureTemp);%属性的个数 newEntropy = 0;%划分之后的熵 for i = 1:numF subSet = splitData(data, j, featureTemp(i,:)); [m_1, n_1] = size(subSet); prob = m_1./m; newEntropy = newEntropy + prob * calEntropy(subSet); end %计算增益 infoGain = baseEntropy - newEntropy; if infoGain > bestInfoGain bestInfoGain = infoGain; bestFeature = j; end end end

function [ subSet ] = splitData( data, axis, value ) [m,n] = size(data);%得到待划分数据的大小 subSet = data; subSet(:,axis) = []; k = 0; for i = 1:m if data(i,axis) ~= value subSet(i-k,:) = []; k = k+1; end end end
