数学瞎整理

 

一.质数

　1.筛质数：有两种 一个线性筛，一个欧拉筛。一般用欧拉筛就行了，如果是求一个[l,r] l r大但差的绝对值小的区间，先用线性筛筛前面，然后用欧拉筛筛后面

　　欧拉筛O(N log log N)：注意每次i循环从2开始 j从i开始 

bool v[N];
int n;
void prime(int n)
{
    memset(v,0,sizeof(v));
    for(int i=2;i<=n;i++)
    {
        if(v[i]) continue;
        cout<<i<<" ";
        for(int j=1;j<=n/i;j++) v[i*j]=1;
    }
}

　　线性筛 O(N)：j从1开始

void primes(int n)
{
    memset(v,0,sizeof(v));
    cnt=0;
    for(int i=2;i<=n;i++)
    {
        if(!v[i]) prime[++cnt]=i,v[i]=i;
        for(int j=1;j<=cnt;j++)
        {
            if(prime[j]>v[i]||prime[j]>n/i) break;
            v[i*prime[j]]=prime[j];
        }
    }
    for(int i=1;i<=cnt;i++)
        cout<<prime[i]<<" ";
}

　2.质因数分解：试除法。 结合欧拉筛，扫描2~ √N的每个数d, 若d整除N,从N中除掉所有因子d，同时累计除去的d的个数。

void divide(int n)
{
    cnt=0;
    for(int i=2;i*i<=n;i++)
    {
        if(n%i==0) 
        {
            prime[++cnt]=i; c[cnt]=0;
            while(n%i==0) n/=i,c[cnt]++;
        }
    }
    if(n>1) prime[++cnt]=n,c[cnt]=1;
    for(int i=1;i<=cnt;i++)
        cout<<prime[i]<<"^"<<c[i]<<endl;
}

　3.example

#include<bits/stdc++.h>
#define ll long long 
#define N 10000010
#define mod 998244353
using namespace std;
ll prime[N],cnt,v[N];
ll L,R,ans,ans2;
void pre()
{
    for(int i=2;i<1000000;i++)
    {
        if(v[i]==0) v[i]=i,prime[++cnt]=i;
        for(int j=1;j<=cnt;j++)
        {
            if(prime[j]>v[i]||prime[j]>1000000/i) break;
            v[i*prime[j]]=prime[j];
        }
    }
}
int main()
{
    pre();
    scanf("%lld%lld",&L,&R);
    memset(v,0,sizeof(v));
    for(ll i=1;i<=cnt;i++)
    {
        ll st=max(1ll,(L-1)/prime[i])*prime[i]+prime[i];
        for(ll j=st;j<=R;j+=prime[i])
        {
            if(v[j-L]) continue;
            v[j-L]=1;
            ans++;
            ans2=(ans2+prime[i])%mod;
        }   
    }
    printf("%lld %lld",ans,ans2);
    return 0;
}

 二.约数

• 求约数（集合）

　　　1.试除法：略

　　　　有一推论：一个整数N的约数个数上界为2√N

　　　2.倍数法

　　　　推论：1~N每个数的约数个数的总和约为 N log N

vector<int> f[N];
int n;
void pu(int n)
{
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n/i;j++)
            f[i*j].push_back(i);
    for(int i=1;i<=n;i++){
        for(int j=0;j<f[i].size();j++)
            cout<<f[i][j]<<" ";
        cout<<endl;
    }
}

 　　　3.example 反素数

　　　　见P134

#include<bits/stdc++.h>
#define N 2000000000
#define ll long long
using namespace std;
ll n;
ll ans;
int num=1;
int a[11]={0,2,3,5,7,11,13,17,19,23,29};
void dfs(int dep,int dex,ll anss,int cnt)
{
    if(dep==10)
    {
        if((anss>ans&&cnt>num)||(anss<=ans&&cnt>=num))
        {
            ans=anss; 
            num=cnt;
        }
        return;
    }
    int t=1;
    for(int i=0;i<=dex;i++)
    {
        dfs(dep+1,i,anss*t,cnt*(i+1));
        t*=a[dep];
        if(anss*t>n) break;
    }
}
int main()
{
    scanf("%lld",&n);
    dfs(1,30,1,1);
    printf("%lld
",ans);
    return 0;
}

• gcd

　　　1.定理：

• gcd(a,b)*lcm(a,b)=a*b

• gcd(a,b)=gcd(b,a-b)=gcd(a,a-b)  (a>=b)

• gcd(a,b)=gcd(b,a mod b) (b!=0)

　　　2.一行gcd:

int gcd(int a,int b)
{
    return b?gcd(b,a%b):a;
}

 　　　3.example hankson

　　　　贼毒了...我是用暴力写的....还用了自带函数__gcd()

#include<bits/stdc++.h>
#define N 20000100
#define ll long long
using namespace std;
ll f[N];
int cnt;
ll a0,a1,b0,b1;
int i;
void div(int x)
{
    cnt=0;
    for(i=1;i*i<=x;i++)
        if(x%i==0)
        {
            f[++cnt]=i;
            if(i!=x/i) f[++cnt]=x/i;
        }
}
ll ans;
void red(ll &x)
{
    ll f=1;x=0;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();}
    while(c>='0'&&c<='9') {x=x*10+c-'0';c=getchar();}
    x*=f;
}
void print(ll x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) print(x/10);
    putchar(x%10+'0');
}
int main()
{
    ll t;
    red(t);
    while(t--)
    {
        red(a0);red(a1);red(b0);red(b1);
        div(b1);
        ans=0;
        for(i=1;i<=cnt;i++)
        {
            ll yy=__gcd(f[i],b0);
            if(b0*f[i]/yy!=b1) continue;
            if(__gcd(f[i],a0)==a1) ans++;
        }
        printf("%lld
",ans);
    }
    return 0;
}

 三.互质和phi

　1.phi(i)指1~i之间与i互质的数个数

　2.

                

　代码如下：

int phi(int n)
{
    int ans=n;
    for(int i=2;i*i<=n;i++)
        if(n%i==0)
        {
            ans=ans/i*(i-1);
            while(n%i==0) n/=i;
        }
    if(n>1) ans=ans/n*(n-1);
    return ans;
}

　3.性质  (p均为质数）

• 任意n>1,1~n中与n互质的数的和为 n * phi(n) / 2 ;
• 若a,b互质，phi(a*b)=phi(a)*phi(b);
• 若p|n 且 p^2|n, 则phi(n)=phi(n/p)*p;
• 若p|n 但不满足 p^2|n，则phi(n/p) * (p-1);
• ∑d|n phi(n)=n;

 

四.同余

• PRE

　　　1.费马小定理：

　　　　　　

　　证明在这里

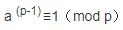
　　　2.欧拉定理：若正整数a,n 互质

　　　　　　

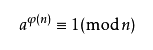
　　　3. 欧拉定理的推论：

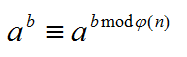　　　(mod n)

　　　由此，我们在计算乘方算式需要取模时，可以先把底数对p取模，指数对phi(p)取模，再计算乘方

• EXGCD和逆元

　　　1.exgcd: 用于计算x,y  使得对于任意整数a,b， 存在一对整数x,y，满足ax+by=gcd(a,b)

　　　　

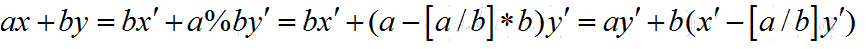
　　　　所以 ：

       　　　　　  

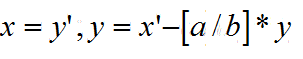
int exgcd(int a,int b,int &x,int &y)
{
    if(b==0) { x=1; y=0;return a; }
    int d=exgcd(b,a%b,y,x);
    y-=a/b*x;
    return d;
}
//d=exgcd(a,b,x0,y0);

 　　　　调用函数可求得 ax + by = gcd (  x,  y ) 的一组特解，d 为 gcd ( a , b )