《DSP using MATLAB》Problem 4.13

     

代码：

%% ----------------------------------------------------------------------------
%%            Output Info about this m-file
fprintf('
***********************************************************
');
fprintf('        <DSP using MATLAB> Problem 4.13 

');

banner();
%% ----------------------------------------------------------------------------


%% -------------------------------------------------
%%              X(z)  rational function
%% -------------------------------------------------

b0 = 2; b1 = 3;         % numerator coefficient
a1 = -1; a2 = 0.81;     % denumerator                 

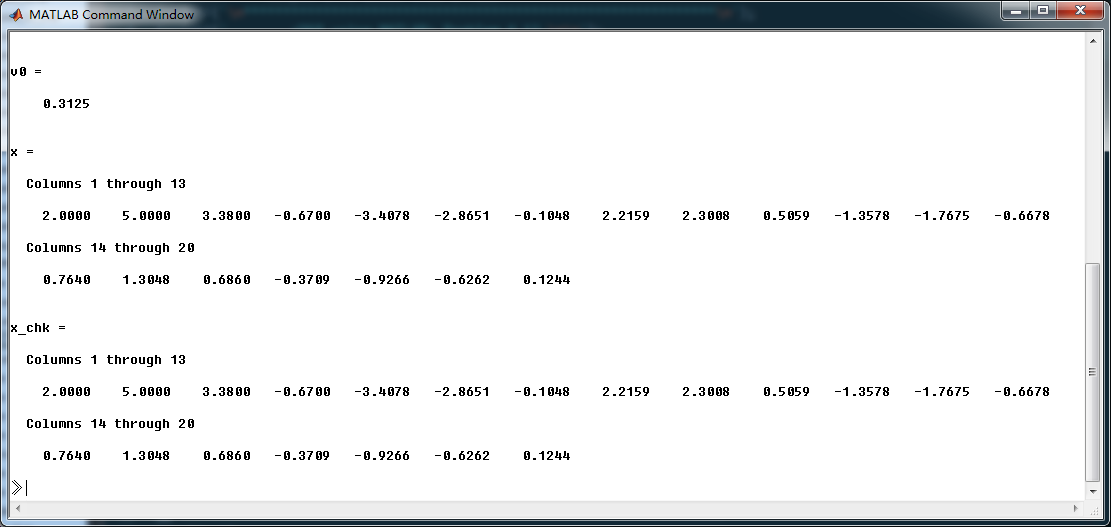
[As, Ac, r, v0] = invCCPP(b0, b1, a1, a2)

%% ------------------------------------------------------------------------
%%       x(n)=Ac*(r^n)*cos(pi*v0*n)*u(n) + As*(r^n)*sin(pi*v0*n)*u(n)
%% ------------------------------------------------------------------------
n_start = 0; n_end = 19;
n = [n_start : n_end];

x = Ac * (r.^n) .* cos( pi * v0 .* n) .* stepseq(0, n_start, n_end) + As * (r.^n) .* sin(pi * v0 .* n ) .* stepseq(0, n_start, n_end)

b = [2, 3]; a = [1, -1, 0.81];
x_chk = filter(b, a, impseq(0, n_start, n_end))

figure('NumberTitle', 'off', 'Name', 'Problem 4.13 x(n)')
set(gcf,'Color','white'); 
stem(n, x);
title('x(n)'); grid on;

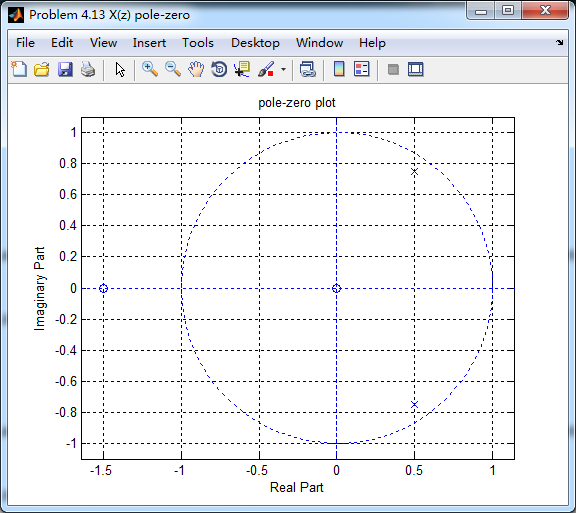
figure('NumberTitle', 'off', 'Name', 'Problem 4.13 X(z) pole-zero')
set(gcf,'Color','white'); 
zplane(b, a);
title('pole-zero plot'); grid on;

　　应用P4.12中的invCCPP函数，计算系数如下：

        序列的前20个样值：