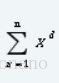"科林明伦杯"哈尔滨理工大学第八届程序设计竞赛——Hrbust -2370 SUM(快速幂)

Description
Calculate MOD 1,000,000,007.(1≤n≤1e5, 1≤d≤1e9)

Input
The first line is an integer t(1≤t≤100), which is the number of test cases.

Then t lines follow. Each line contains two numbers n and d.

Output
T lines, which are the answers.

Sample Output
3

2 3

3 2

4 1

Hint
9

14

10

题意：给出x和d，对x从1到x的d次方求和
就是快速幂模板。。。加和都是用for的O(n)的跑一边。。。一开始第一题做这个超时了，就慌了，根本想不到任何优化的方法，想预处理也不可能。后面先写其他题了。最后实在没办法了，去掉了两个看似多余的取模又交了一次，竟然过了。。。虽然这题给了10秒，轮取模的耗时。。。

#include<stdio.h>
#include<string.h>
#define LL long long
using namespace std;
const LL MOD=1000000007;
LL a[100008];
LL poww(LL a,LL b)
{
    LL ans=1;
    while(b)
    {
        if(b&1)ans=(ans*(a%MOD))%MOD;///多次取模会超时
        a=(a*(a%MOD))%MOD;
        b>>=1;
    }
    return ans;
}
int main()
{
    int t;
    LL n,d;
    scanf("%d",&t);
    while(t--)
    {
        LL sum=1;
        scanf("%lld%lld",&n,&d);
        for(int i=2; i<=n; i++)
        {
            sum=(sum+poww(i,d)%MOD)%MOD;///多次取模会超时
        }
        printf("%lld
",sum);
    }
}