Farmer John has noticed that the quality of milk given by his cows varies from day to day. On further investigation, he discovered that although he can’t predict the quality of milk from one day to the next, there are some regular patterns in the daily milk quality.
To perform a rigorous study, he has invented a complex classification scheme by which each milk sample is recorded as an integer between 0 and 1,000,000 inclusive, and has recorded data from a single cow over N (1 ≤ N ≤ 20,000) days. He wishes to find the longest pattern of samples which repeats identically at least K (2 ≤ K ≤ N) times. This may include overlapping patterns – 1 2 3 2 3 2 3 1 repeats 2 3 2 3 twice, for example.
Help Farmer John by finding the longest repeating subsequence in the sequence of samples. It is guaranteed that at least one subsequence is repeated at least K times.
Input
Line 1: Two space-separated integers: N and K
Lines 2… N+1: N integers, one per line, the quality of the milk on day i appears on the ith line.
Output
Line 1: One integer, the length of the longest pattern which occurs at least K times
Sample Input
8 2
1
2
3
2
3
2
3
1
Sample Output
4
题意:输入一个长度为n的序列,在序列中找一个最长的重复k次的子序列,输出重复K次的序列的长度。
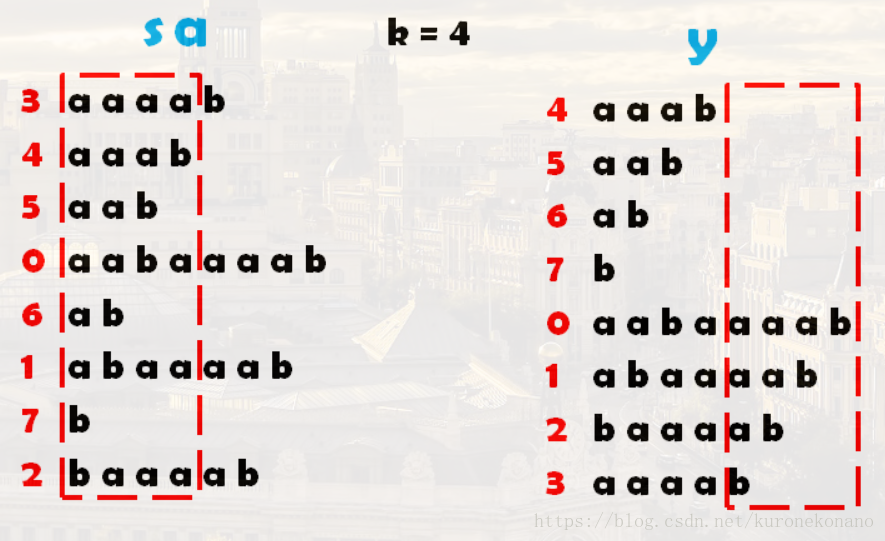
思路:利用后缀数组可以求得height数组得到最长公共前缀,通过计算最长公共前缀中各个子串公共前缀的长度出现次数,二分出最大的满足要求重复次数的 子序列长度。
下面介绍后缀数组:
首先我们要明确,后缀数组,顾名思义即对于一个串的处理,一个串长度为n,那么该串就有n个长度不同的后缀,而后缀数组表示的就是该串中所有后缀的信息。一个串的某个后缀是一个起点为i终点为n的子串,我们此时不记录该串完整的后缀,我们用该串开始的位置i来表示每一个不同的后缀,即有i即可明确是哪一个后缀。
举个例子,首先我们给出一个串 a a b a a a a b
完整的列出该串的每一个后缀,即:
我们用该串的下标i来命名每一个后缀,可以观察一下,横着看是从串本身开始依次长度减少的每一个后缀,我们发现,**竖着看每一行的第一个首字符,也就是第一列,完整的表示了整个串的原串。**这个特征在后面的排序部分有不可忽视的作用。
知道了后缀的意义,下面介绍后缀数组实现的功能。
后缀数组所实现的功能是将一个串的所有后缀按字典序进行排序。也就是构造一个数组,这个数组表示了每一个后缀他在所有后缀中按字典序排列可以排第几。 利用这层关系,我们可以继续求出LCP最长公共前缀。以及其他信息。换句话说,后缀数组实现的基本目的即对后缀排序。
具体到能解决什么问题可点击这个链接
知道了后缀的功能,下面开始认识一下后缀数组的组成。
**1. 后缀数组(SA[i]存放排名第i大的后缀首字符下标) **
后缀数组 SA 是一个一维数组,它保存1…n 的某个排列 SA[1] ,SA[2] , ……, SA[n] ,并且保证Suffix(SA[i]) < Suffix(SA[i+1]), 1 ≤ i < n 。也就是将 S 的 n 个后缀从小到大进行排序之后把排好序的后缀的开头位置顺次放入SA 中。
2. 名次数组(rank[i]存放各个后缀的优先级)
名次数组 Rank[i] 保存的是 以下标 i 开头的后缀在所有后缀中从小到大排列的 “ 名次 ” 。
可以看出Rank数组和SA数组为互逆的运算,两者相互映射。若已知其中一个数组,即可求出另一个数组。同时我们也可以用一个数组对应的值去指定另一个数组对应的值。
最后总结为 :
SA[i] = j表示为按照从小到大排名为i的后缀 是以j(下标)开头的后缀
rank[i] = j 表示为按照从小到大排名 以i为下标开始的后缀 排名为j
①**RANK表示你排第几 **
SA表示排第几的是谁
② RANK数组中下标表示每个后缀的下标,对应的值表示序号为i的后缀的排名
SA数组中下标表示排名,对应的值为后缀的序号,表示排名为i的后缀是谁
③RANK数组中后缀是有序的,排名是无序的
SA数组中排名是有序的,后缀是无序的
tax数组:用于计数排序,存储了字符出现次数的前缀和
tp数组:用于计数排序,实现的功能和SA数组一样,但tp数组是一个第二关键字的后缀数组,可以理解为SA数组求解过程中的一个临时存储,并辅助后续求解。我们将用tp数组表示排序排到一半时,用于承上启下的信息存储。简单的说,即第二关键字后缀数组,联立第一关键字后缀数组可以合并前后两关键字的信息并做新的排序。
str字符数组:用于存储原字符串。
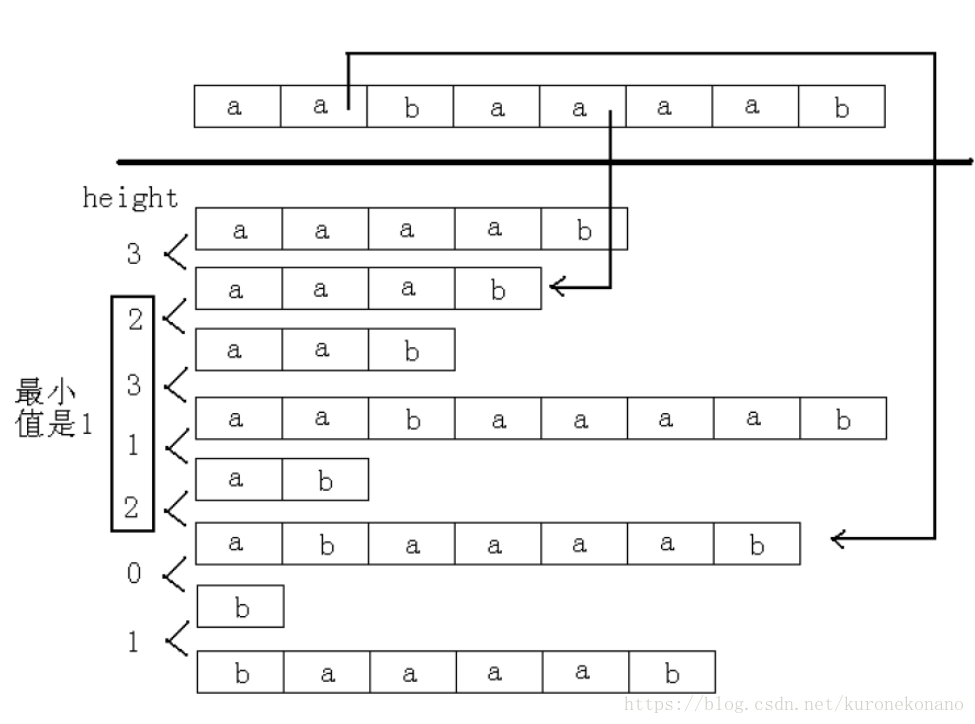
Heigth[i]相邻排名最长公共前缀数组 : 表示Suffix[SA[i]]和Suffix[SA[i - 1]]的最长公共前缀,也就是排名相邻的两个后缀的最长公共前缀
H[i] : 等于Height[Rank[i]],也就是后缀Suffix[i]和它前一名的后缀的最长公共前缀
而两个排名不相邻的最长公共前缀定义为排名在它们之间的Height的最小值。
以上即后缀数组求解过程中需要用到的几个重要的组件。
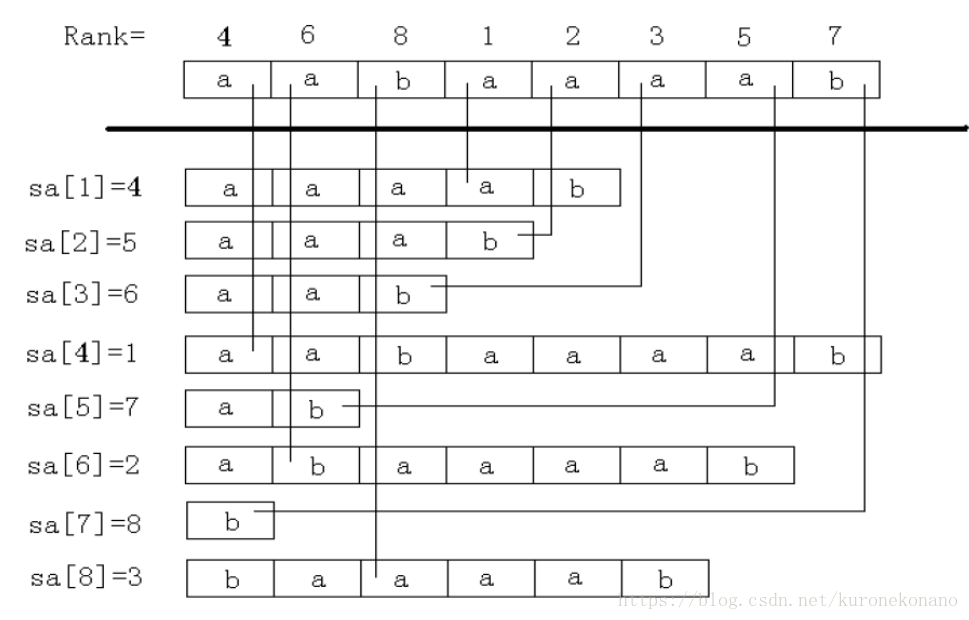
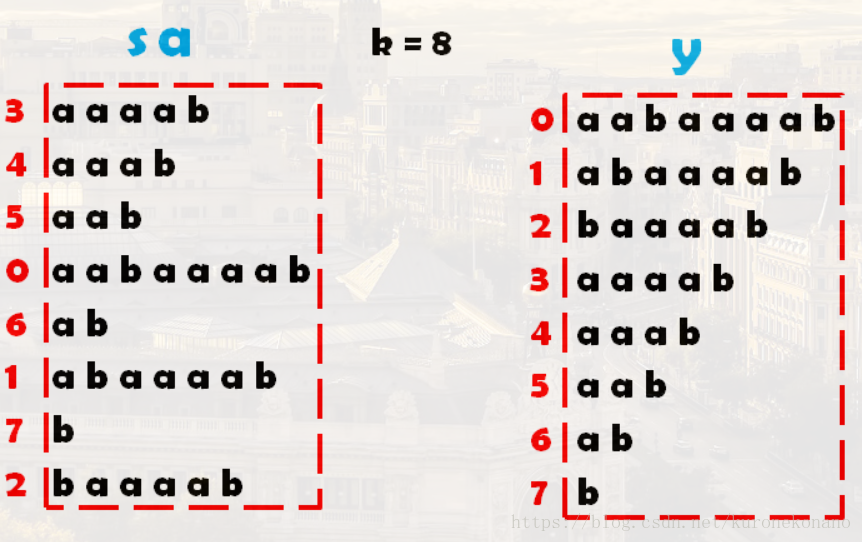
上面提到的SA数组即后缀数组。最终结果表示排序的信息。仍是aabaaaab 这个例子,我们求出的最终结果应是这样的:
如何快速构造这样的排序信息的数组?
①基数排序
我们先要了解一下基数排序:
基数排序(对于两位数的数复杂度就是O(Len)的)。
基数排序原理 : 把数字依次按照由低位到高位依次排序,排序时只看当前位。对于每一位排序时,因为上一位已经是有序的,所以这一位相等或符合大小条件时就不用交换位置,如果不符合大小条件就交换,实现可以用”桶”来做。
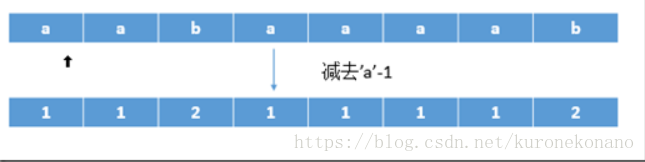
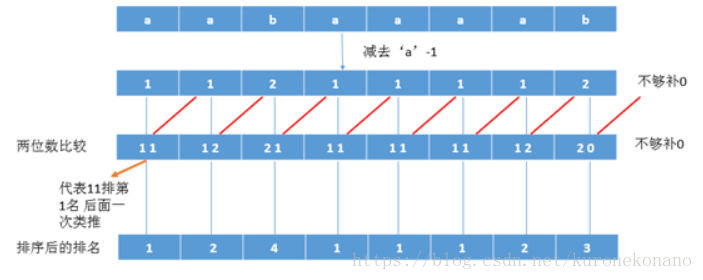
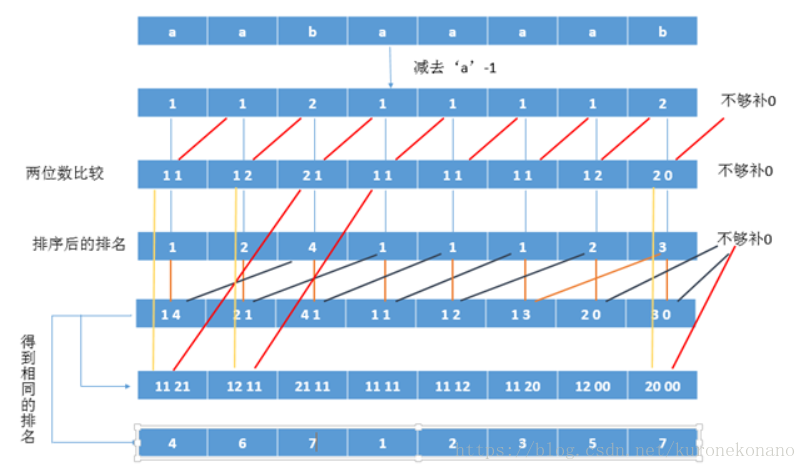
具体来说:对于字符串aabaaaab,我们先将字母转换为数字。直接减去’a’-1即可。然后再进行基数排序的操作。
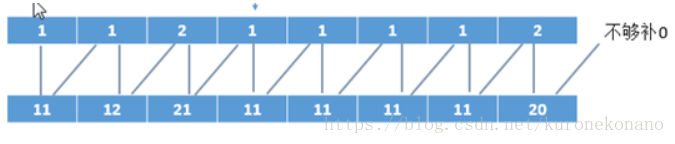
下面将相邻俩个数合并为一个整数
这样下面使用基数排序对这个合并后的整数进行排序 为什么使用基数排序 因为它的位数固定 也许你会问那
字母 ‘z’ 减去‘a’- 1 不是大于10了吗 那不是3位数了吗 不是这样的 把 z 减去‘a’- 1 =26 看做是一个数 而不是二十六
将相当于16进制 一样15不是看做两位数 而是用F来表示 当然你高兴 完全可以把26写作Z以后 Z就是26
下面我讲解一下 这个很重要 为什么要两两合并为一个数
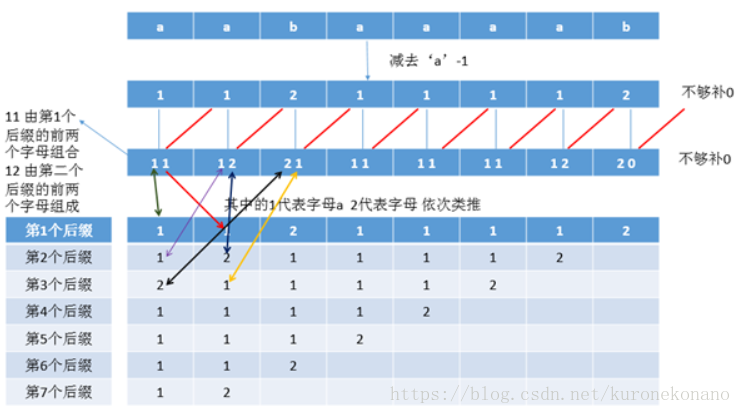
首先求所有后缀数组最后组成为下图
那么每一个后缀之间都是有重复的 第1个后缀的前两个就是第0个后缀的第一到第三个字母。
那么一次类推 也就是说我按下图分为两两一组 一个整数按照基数排序的结果为
解释一下 第一个11 排第一名 第二个12 排第二名
那么你有没有发现第0个后缀到第7个后缀的前两个字母的比较已经出来了 因为第一个11 就是第1个后缀的前两个字母 第二个12 就是第2个后缀的前两个字母
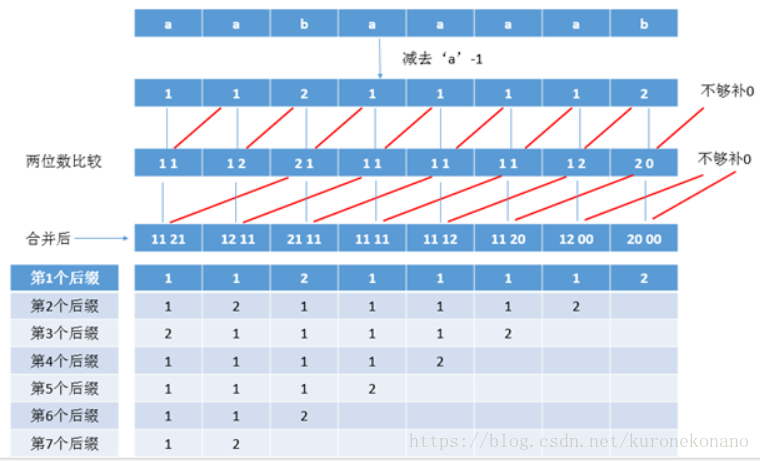
好了 现在我们已经比较所有后缀的前两个字母 下面我开始比较后面 那么我怎么比较前两个字母后面的字符串呢 因为刚才我已经把所有的两两字母的大小已经比较出来了 我现在可以利用下面的结果再比较 看图 其中合并后的 1121 就是第一个后缀的前四个字母 1211 就是第二个后缀的前四个字母
下面开始再次拼接 如图 最后这号拼成八位数 也就是正好字符串的长度 这时候可以使用基数排序来比较 但是假如字符串10000个呢 那么有10000个后缀 每个后缀的长度是10000 意味着最后拼接成的数也是有10000位 10000*10000我们需要开辟这么大数据这是不可行的 那么我们能不能将每次拼接的大数缩小呢?
首先后缀数组最终要获得的是后缀的排名 那么到底是1112 还是 11 是1221 还是24 无所谓
我只要把他们保持合适的大小 就比如说 小明考了100分 小红考了89分 小刚考了55分
那么我现在把小刚设为0分 小红设为1分 小明设为2分 那么对他们最后的排名有影响吗 没有
小明还是第一名 就是这个道理 这样我们可以最大程度减小存储的开销
所以我只要每次对合并的数据进行按照从小到大排个序 用序号替换它 然后再次按照之前的步骤再次合并 再次排序替换 (什么时候结束)当全部的字符串都参与了比较就停止了
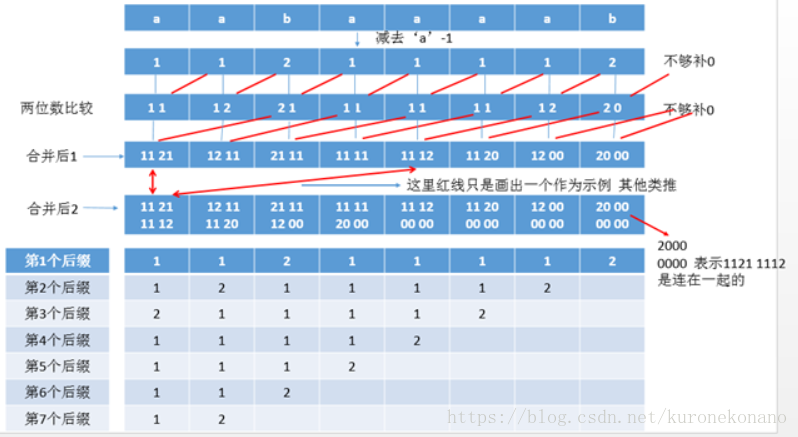
那么现在对1121 1211 2111 1111 1112 1120 1200 2000进行排序 分成两组 前两个字母一组后两个字母一组 比如 1121这四个数字 11 与 21 两份来基数排序
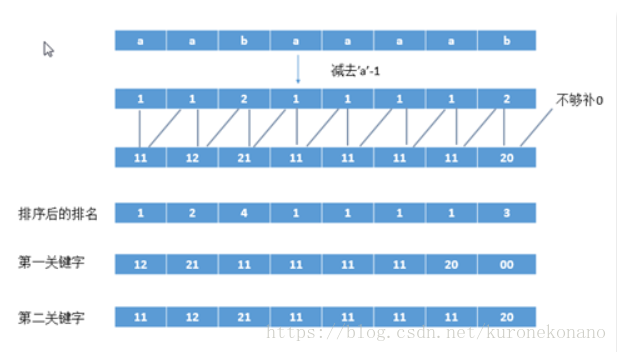
等等 ,你有没有发现 我们上面的排序后的排名,跟第一关键字与第二关键字有关系,也就是说
排名的大小就是第二关键字排名的 ,为什么? 因为排序后的排名就是 第二关键字的排序结果
那么与第一关键字有什么关系 ? 有没有发现,就是把第一关键字的11去掉,然后再加一个00
举个生动的例子 ,现在有很多人在排队 ,高矮不等 ,一开始是乱序的 ,现在保安要求按从矮到高排列。
排好序之后 ,大家都有了自己的位置 ,现在保安走开了,队伍又回到一开始的状态, 并且原来站在最开始的人(乱序时站在最开始的人)走了 【除去第一关键字】,来了一个小矮人【对第二关键字排序】,肯定是最矮的 ,保安回来,要求再次排队 ,那么小矮人肯定站在最前面 ,下面保安喊道,上次排序排第一的人接上 ,如果走的那个人是第一 ,那么就继续后面 如果不是上次排名第一的人就站上来 ,然后保安继续叫 ,一直到上次排名最后的一个。
②倍增算法
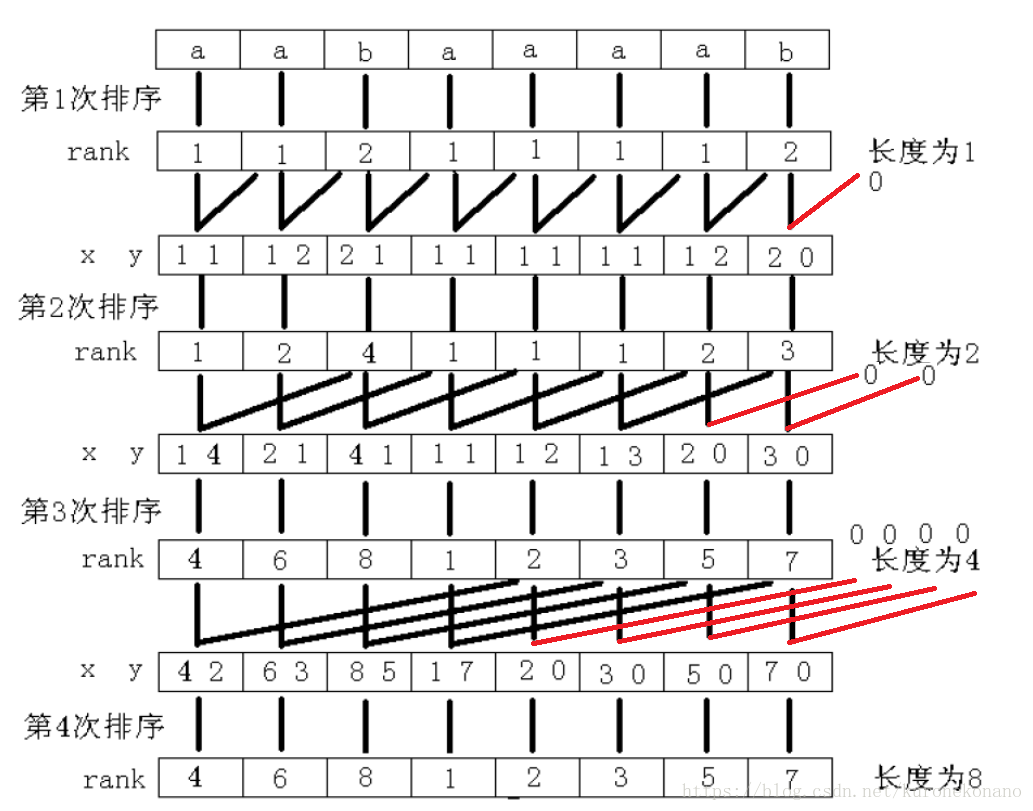
倍增算法的主要思想 :对于一个后缀Suffix[i],如果想直接得到Rank比较困难,但是我们可以对每个字符开始的长度为2k的字符串求出排名,k从0开始每次递增1(每递增1就成为**一轮**),当2k大于Len时,所得到的序列就是Rank,而SA也就知道了。O(logLen)枚举k 。
这样做有什么好处呢?
设每一轮得到的序列为rank(注意r是小写,最终后缀排名Rank是大写)。有一个很美妙的性质就出现了!第k轮的rank可由第k - 1轮的rank快速得来! 【这里说明的是,我们每次对下一轮的排序,其实并不是排序,而是通过向后挪动当前排序结果而得到的下一轮排序,这个所谓下一轮排序即第二关键字的排序。也就是tp数组】
为什么呢?为了方便描述,设SubStr(i, len)为从第i个字符开始,长度为len的字符串我们可以把第k轮SubStr(i, 2^k)看成是一个由SubStr(i, 2^(k−1))和SubStr(i + 2^(k−1), 2(k−1))**拼起来的东西。类似**rmq算法**,这两个长度而2(k−1)的字符串是上一轮遇到过的!当然上一轮的rank也知道!**那么吧每个这一轮的字符串都转化为这种形式,并且大家都知道字符串的比较是从左往右,左边和右边的大小我们可以用上一轮的rank表示,那么……这不就是一些两位数(也可以视为第一关键字和第二关键字)比较大小吗!再把这些两位数重新排名就是这一轮的rank。 【这里如果不好理解可以回想一下开始介绍后缀时注意到的特征,对于每一个后缀的开头第一个字符,我们竖着观察发现能凑出一个完整的原串,这启发我们,因为我们求的后缀是同一个串的,也就是说,一个后缀,不止是原串的后缀,还是前几个后缀的后缀,那么如果我们已经对其进行遍历过,并且拍好序的一些后缀,我们没有必要对其再重新排序,而是在原来基础上,去除因长度而排名前移的后缀,剩余后缀在保持相对位置的基础上,直接将排名后挪,即可得到第二关键字的新排序,说是新排序,其实相对第一关键字排序来说,只是去除了一定影响,继续爆保持原来的相对位置的一种排列,说白了就是一些人以为重组而排名靠前了,那么剩余的人没有什么重组的改变,那么这些人的相对位置仍是不变的,这些人在原有排序的基础上,给排名靠前的人挪出位置就好了。不用重新再给他们排序。】
至此,通过倍增法优化的基数排序整个过程介绍完毕,整个过程及最终结果如图:
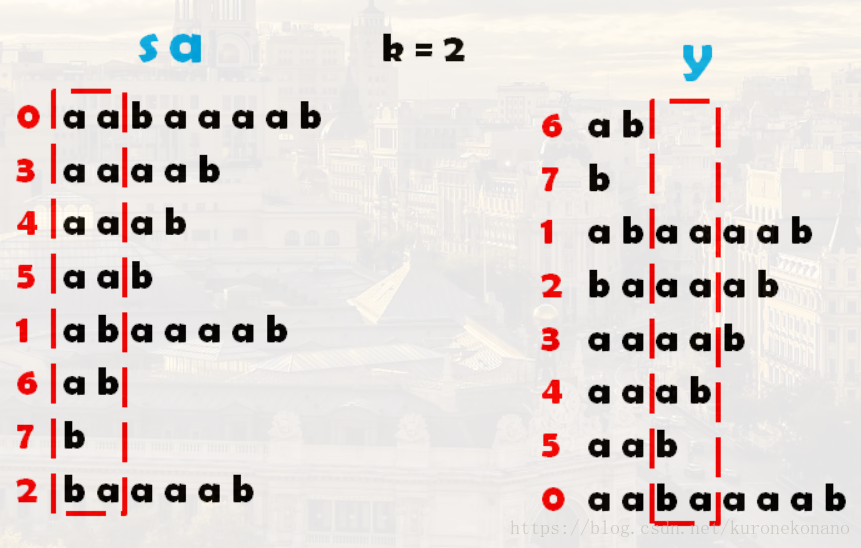
以上方法提供了转化为数字后在数组中是如何排序的。那么在排序过程中,我们选择的关键字,在排序过程中的后缀字符串是怎样变化的?过程如下:【可以手动模拟一下理解效果更佳】
转自:https://blog.csdn.net/Bule_Zst/article/details/78604864#insertcode
https://www.cnblogs.com/nietzsche-oier/articles/6621881.html
https://blog.csdn.net/yxuanwkeith/article/details/50636898#t8
代码如下:
#include<stdio.h>
#include<algorithm>
#include<string.h>
using namespace std;
const int Maxn=20005;
int a[Maxn],SA[Maxn],rank[Maxn],tax[1000006],tp[Maxn],height[Maxn],n,m;
void Rsort()
{
for(int i=0; i<=m; i++)tax[i]=0;
for(int i=1; i<=n; i++)tax[rank[tp[i]]]++;
for(int i=1; i<=m; i++)tax[i]+=tax[i-1];
for(int i=n; i>=1; i--) SA[tax[rank[tp[i]]]--]=tp[i];
}
void SSA()
{
for(int i=1; i<=n; i++)tp[i]=i;
m=1000000;
Rsort();
int p=1,i;
for(int dis=1; p<n; dis+=dis,m=p)
{
for(p=0,i=n-dis+1; i<=n; i++)tp[++p]=i;
for(i=1; i<=n; i++)
if(SA[i]>dis) tp[++p]=SA[i]-dis;
Rsort();
swap(rank,tp);
rank[SA[1]]=p=1;
for(int i=2; i<=n; i++)
rank[SA[i]]=(tp[SA[i]]==tp[SA[i-1]]&&tp[SA[i]+dis]==tp[SA[i-1]+dis])?p:++p;
}
int j,k=0;
for(i=1; i<=n; height[rank[i++]]=k)
for(k =k?k-1:0, j=SA[rank[i]-1]; a[i+k]==a[j+k]; ++k);
}
bool judge(int len,int k)
{
int i=1,cnt=0;
for(int i=1;i<=n;i++)
{
if(height[i]>=len)
{
cnt++;
if(cnt+1>=k)return true;
}
else cnt=0;
}
return false;
}
int main()
{
int cnt[Maxn],k;
while(scanf("%d%d",&n,&k)!=EOF)
{
if(n==0)break;
memset(cnt,0,sizeof(cnt));
for(int i=1; i<=n; i++)
{
scanf("%d",&a[i]);
rank[i]=a[i];
}
SSA();
// for(int i=1;i<=n;i++)
// {
// printf("%d %d ",height[i],i);
// for(int j=SA[i];j<=n;j++)printf("%d",a[j]);
// printf("
");
// }
for(int i=1;i<=n;i++) cnt[height[i]]++;
int l=1,r=n,mid,ans=0;
while(l<=r)
{
mid=(l+r)/2;
if(judge(mid,k)) l=mid+1,ans=mid;
else r=mid-1;
}
printf("%d
",ans);
}
}
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAXN = 100005;
char ch[MAXN], All[MAXN];
int SA[MAXN], rank[MAXN], Height[MAXN], tax[MAXN], tp[MAXN], a[MAXN], n, m;
char str[MAXN];
///rank[i] 第i个后缀的排名; SA[i] 排名为i的后缀位置; Height[i] 排名为i的后缀与排名为(i-1)的后缀的LCP
///tax[i] 计数排序辅助数组,字符出现次数前缀和; tp[i] rank的辅助数组(计数排序中的第二关键字),与SA意义一样。
///a为原串
void RSort()
{
///rank第一关键字,tp第二关键字。
for (int i = 0; i <= m; i ++) tax[i] = 0;
for (int i = 1; i <= n; i ++) tax[rank[tp[i]]] ++;///遍历字符数组,给每个字符的出现次数计数
for (int i = 1; i <= m; i ++) tax[i] += tax[i-1];///累加求和变为前缀和
for (int i = n; i >= 1; i --) SA[tax[rank[tp[i]]]--] = tp[i]; ///确保满足第一关键字的同时,再满足第二关键字的要求
} ///计数排序,把新的二元组排序。
int cmp(int *f, int x, int y, int w)///两个相邻排名的后缀,x=i,y=i-1,即较后的排名与较前的排名的两后缀的字符,比较他们的第一关键字的排名(rank)
{
return f[x] == f[y] && f[x + w] == f[y + w];
}
///通过二元组两个下标的比较,确定两个子串是否相同
void Suffix()
{
///SA
for (int i = 1; i <= n; i ++) rank[i] = a[i], tp[i] = i;///tp数组为第二关键字的排名,那么初始化没有第二关键字,排名从1到n
///rank表示第i个后缀排第几,初始化第i个后缀排名为他的ascii值
m = 127,RSort(); ///一开始是以单个字符为单位,所以(m = 127),基数排序,以单字为单位的SA同时构造
int p=1;///P是一个构造的指针
for (int w = 1; p < n; w += w, m = p) ///把子串长度翻倍,更新rank,w表示翻倍的长度
{
int i;
///w 当前一个子串的长度; m 当前离散后的排名种类数
///当前的tp(第二关键字)可直接由上一次的SA的得到
for (p = 0, i = n - w + 1; i <= n; i ++)
tp[++ p] = i; ///长度越界,第二关键字为0,tp表示第二关键字的排名,那么第二关键字为0的排名必定靠前
printf("--------------first-------------
");
for(int i=1; i<=n; i++) printf("%d%c",tp[i],i==n?'
':' ');///根据第二关键字补0排序后的tp数组
for (i = 1; i <= n; i ++)///遍历SA数组
if (SA[i] > w) tp[++ p] = SA[i] - w;
///更新SA值,并用tp暂时存下上一轮的rank(用于cmp比较)
printf("--------------second-------------
");
for(int i=1; i<=n; i++) printf("%d%c",tp[i],i==n?'
':' ');
RSort();
swap(rank, tp);
rank[SA[1]] = p = 1;///更新rank[]=1的位序,也就是找到排第一的是谁,先安排好
///用已经完成的SA来更新与它互逆的rank,并离散rank
for (i = 2; i <= n; i ++) rank[SA[i]] = cmp(tp, SA[i], SA[i - 1], w) ? p : ++ p;
///从排第二的后缀开始比较,离散与更新rank数组,利用SA数组进行更新,因为SA表示相邻排名的两后缀,我们利用的是上一轮的rank加上最新的SA数组判断 此处计算的是排名
printf("..................rank..................
");
for(int i=1; i<=n; i++) printf("%d%c",rank[i],i==n?'
':' ');
}
///离散:把相等的字符串的rank设为相同。
///LCP
int j, k = 0;
for(int i = 1; i <= n; Height[rank[i ++]] = k)
for( k = k ? k - 1 : k, j = SA[rank[i] - 1]; a[i + k] == a[j + k]; ++ k);
///这个知道原理后就比较好理解程序
}
void Init()
{
scanf("%s", str);///输入字符串
n = strlen(str);
for (int i = 0; i < n; i ++) a[i + 1] = str[i];///将字符串的每个字符挪到a串上,从1开始到n结束
}
int main()
{
Init();
Suffix();
int ans = Height[2];
for (int i = 3; i <= n; i ++) ans += max(Height[i] - Height[i - 1], 0);
printf("%d
", ans);
}
///rank表示第一关键字的第i个后缀的排名,因为是有延迟的更新,因此在tp表示第二关键字的时候rank还在表示第一关键字
///那么就可以根据rank和tp联合在一起的数据表示第一第二关键字的总排名
///关于第二关键字,不是排序拍出来的,是根据第一关键字的排名SA进行后移挪出来的排名,因为可以发现第一关键字就包括了所有后缀的情况
///只要将第一关键字被排名的一段后缀的排名后挪,将没有第二关键字的后缀前挪,即利用SA数组即可求出tp数组
///第二轮排SA数组将根据第二关键字的TP数组给出的顺序来遍历每个后缀的第一关键字符,
///这样在第二关键字中排序靠后的字符将在并列的第一关键字中被优先遍历到,被分配到较后的位置。而原本就最后的第一关键字,无论第二关键字如何,都会被直接挪到最后