In this problem, you have to analyze a particular sorting algorithm. The algorithm processes a sequence of n distinct integers by swapping two adjacent sequence elements until the sequence is sorted in ascending order. For the input sequence
9 1 0 5 4 ,
Ultra-QuickSort produces the output
0 1 4 5 9 .
Your task is to determine how many swap operations Ultra-QuickSort needs to perform in order to sort a given input sequence.
Input
The input contains several test cases. Every test case begins with a line that contains a single integer n < 500,000 – the length of the input sequence. Each of the the following n lines contains a single integer 0 ≤ a[i] ≤ 999,999,999, the i-th input sequence element. Input is terminated by a sequence of length n = 0. This sequence must not be processed.
Output
For every input sequence, your program prints a single line containing an integer number op, the minimum number of swap operations necessary to sort the given input sequence.
Sample Input
5
9
1
0
5
4
3
1
2
3
0
Sample Output
6
0
题意:给出一个序列,求该序列的逆序数。
首先是树状数组求法:
因为有5e5个值,数据范围却有9e9,因此要用树状数组求逆序数需要先进行离散化,只有5e5个数,那么一些较大的数可以根据其相对大小进行离散。缩减到5e5个值之内。
逆序数是根据数字输入的先后顺序,利用树状数组更新和检查每次输入一个新的数时,在其之前输入的比他小的数的个数,即该数的逆序数。
此题中每个数都是唯一的,因此可以用数值的标号进行离散化。需要的信息仅仅是数值的相对大小,而不是数值本身,我们将数值映射到一个小于5e5的数上,使得该数在大小上仍保持原数值性质,但是因为值变小了更利于记录和保存。
首先因为是利用标号进行离散,因此记录下排序前的标号,根据数值大小进行排序,然后,遍历排序后的数组,在一个新的离散数组中,按排序好的顺序记录每个值的标号。如第一个遍历的肯定是最小的值,那么我们再该值原先的位置a[i].i记录下其被映射到的标号1,然后下一个值映射相对第二个值也是新的标号,2,说明其实第二小的数。将其记录到原数值中应有的位置。实现离散化。
对于出现多个重复的数时,就不能用标号来记录相对的大小了,因为标号是唯一的,对于一个完全相同的值,还是会被映射到大小不同的标号上,影响其相对大小。因此我们记录一个num值表示这是第几个不同的值,在遍历有序数组的过程中,每次遇到一个和之前不同的值,num++,并给几个完全相同值映射。实现相同数字的离散化
#include<stdio.h>///树状数组求逆序数+数据离散化
#include<string.h>
#include<algorithm>
using namespace std;
struct num
{
int n,i;
}a[500005];
int tree[500005],ls[500005],n;
int lowbit(int x)///树状数组求逆序数,树状数组记录某个数值是否出现过
{
return x&(-x);
}
int sum(int p)
{
int sum=0;
while(p>0)
{
sum+=tree[p];
p-=lowbit(p);
}
return sum;
}
void update(int p)
{
while(p<=n)
{
tree[p]++;
p+=lowbit(p);
}
}
bool cmp(num a,num b)
{
return a.n<b.n;
}
int main()///数据范围9e9很大,但是数据元素只有5e5个,并且每个元素唯一,因此将所有元素映射到一个5e5之内的数即是离散化,避免空间浪费
{
while(scanf("%d",&n)&&n)
{
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i].n);///记录每个元素的位序,按数值大小排序,按数值从小到大遍历,将数值按位序重新标记成一个较小的数。各个数值大小关系不变
a[i].i=i;
}
sort(a+1,a+n+1,cmp);
for(int i=1;i<=n;i++) ls[a[i].i]=i;///离散化
memset(tree,0,sizeof(tree));
long long ans=0;
for(int i=1;i<=n;i++)
{
update(ls[i]);///按数值从小到大遍历数据,更新当前遍历数字位序的状态,使之变成出现过
ans+=i-sum(ls[i]);///sum求和,计数在ls[i]出现之前,先出现的小于ls[i]的数的个数,这些是正常位序
}///当前遍历的数字数量i,是目前出现的数总数,用i减去正常出现的数的个数,剩余数量就是在ls[i]出现之前
printf("%lld
",ans);///优先出现的大于ls[i]的数值数量,这就是ls[i]的逆序数,不断对ans累加就是结果
}
}
接触树状数组两年之后,才去看归并排序的写法,一直以为非常复杂,其实就是利用归并排序的过程,模板一点都没改,加了句 求ans而已。
下面解释过程:
首先是归并排序的过程,利用了分治的思想
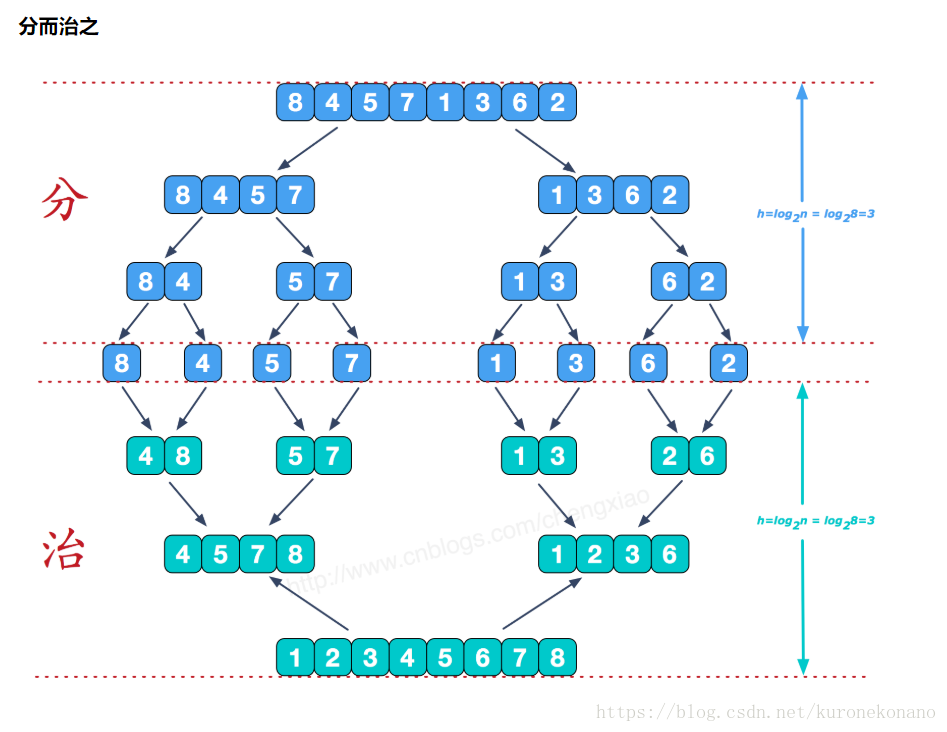
上图清晰的展示了归并排序的步骤,我们计算逆序数的过程在下方的“治”中。也就是合并数组的过程中。首先我们知道,在合并的过程中,两个被合并的子数组是有序的通过不断对比两数组的值来确定合并数组的排列顺序。
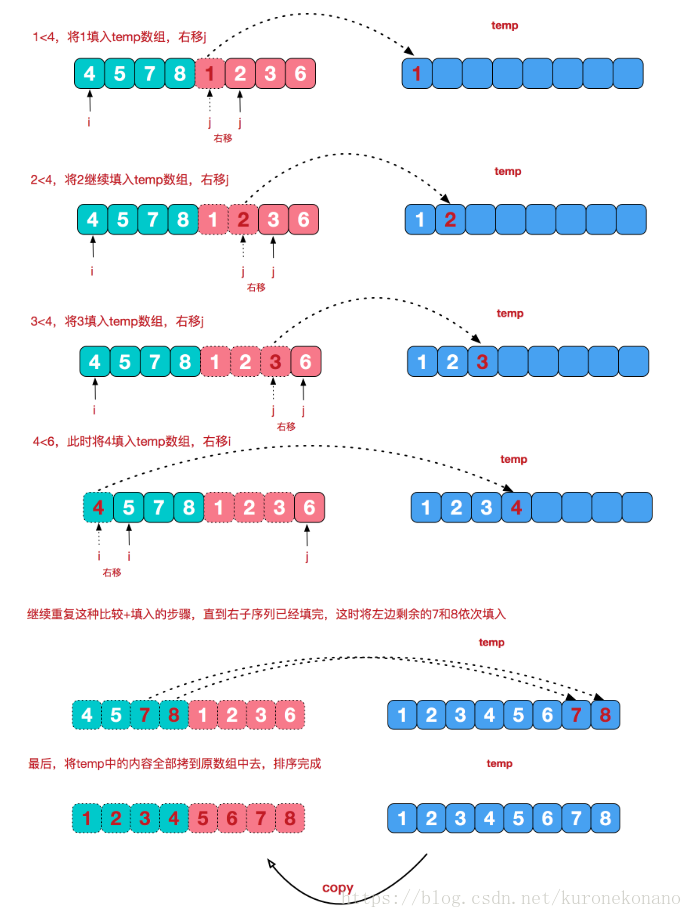
上图中,展示 了合并的详细过程,计算逆序数,即从这里入手。i表示L区间内数组指针,j表示R区间内数组指针,现在两区间内是有序排列,区间之间数字无序,但L区间值在R区间值左边。若当 a【i】>a【j】时,说明a【i】以及a【i】之后的值都大于a【j】(因为有序),并且在位置上L区间内每一个值都在其左边,也就是说,a【j】对于mid-i+1这段区间内所有值都贡献出了一个逆序数。因此逆序数加mid-i+1。
对于所有排序过程中符合条件的值都进行如上求和计算。总和即逆序数值。
相比树状数组求逆序数,归并排序代码简单,不用离散化,使用方便,更加优秀。
代码如下:
#include<bits/stdc++.h>
#define LL long long
#define M(a,b) memset(a,b,sizeof a)
using namespace std;
const int maxn=5e5+7;
int a[maxn],tmp[maxn];
int n;
LL ans;
void Meg(int l,int mid,int r)
{
int i=l,j=mid+1,k=0;
while(i<=mid&&j<=r)
{
if(a[i]<a[j]) tmp[k++]=a[i++];
else
{
ans+=mid-i+1;///逆序数计数
tmp[k++]=a[j++];
}
}
while(i<=mid) tmp[k++]=a[i++];
while(j<=r) tmp[k++]=a[j++];
for(int i=l,k=0;i<=r;k++,i++) a[i]=tmp[k];
}
void Msort(int l,int r)///归并排序模板
{
if(l<r)
{
int mid=(l+r)>>1;
Msort(l,mid);
Msort(mid+1,r);
Meg(l,mid,r);
}
}
int main()
{
while(scanf("%d",&n)&&n)
{
ans=0;
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
Msort(1,n);
printf("%lld
",ans);
}
}