问题描述:给定K个整数组成的序列{ N1, N2, ..., NK },“连续子列”被定义为{ Ni, Ni+1, ..., Nj },其中 1≤i≤j≤K。“最大子列和”则被定义为所有连续子列元素的和中最大者。例如给定序列{ -2, 11, -4, 13, -5, -2 },其连续子列{ 11, -4, 13 }有最大的和20。现要求你编写程序,计算给定整数序列的最大子列和。
1.穷举法:时间复杂度O(n^3)
穷举法,计算了所有可能性,时间复杂度O(n^3)。
1 int MaxSubseqSum1(int a[],int size) 2 { 3 int ThisSum,MaxSum=0; 4 for(int i = 0;i < size;i++) 5 for(int j = i;j < size;j++) 6 { 7 ThisSum = 0; 8 for(int k = i;k <= j;k++) 9 ThisSum += a[k]; 10 if(MaxSum < ThisSum) 11 MaxSum = ThisSum; 12 } 13 return MaxSum; 14 }
2.算法二:时间复杂度O(n^2)
在穷举法的基础上略有改进,少了一重for循环,效率有所提高,代码简单易懂。
int MaxSubseqSum2(int a[],int size) { int ThisSum,MaxSum=0; for(int i = 0;i < size;i++) { ThisSum = 0; for(int j = i;j < size;j++) { ThisSum += a[j]; if(MaxSum < ThisSum) MaxSum = ThisSum; } } return MaxSum; }
3.分而治之:时间复杂度O(nlogn)
采用递归的思想。最大子列和有三种情况,左边最大子列和,右边最大子列和,跨越中间的最大子列和,取三之大者。递归到最后即,两个数,比较左数右数或他们的和,取大。
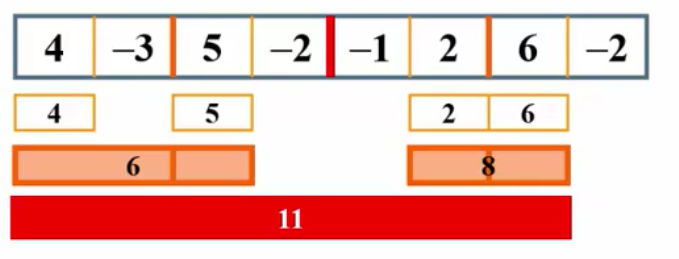
1 //分而治之 2 int MaxSubseqSum3(int a[],int size) 3 { 4 return MaxSum(a,0,size-1); 5 } 6 7 int MaxSum(int a[],int left,int right) 8 { 9 if(left == right) 10 return a[left] > 0 ? a[left] : 0; 11 int center = (left + right) / 2; 12 int MaxLeftSum = MaxSum(a,left,center); 13 int MaxRightSum = MaxSum(a,center+1,right); 14 //求左边界最大值 15 int Centerto_Left = 0,MaxSum_Centerto_Left = 0; 16 for(int i = center;i >= left;i--){ 17 Centerto_Left += a[i]; 18 if(MaxSum_Centerto_Left < Centerto_Left) 19 MaxSum_Centerto_Left = Centerto_Left; 20 } 21 // 求右边界最大值 22 int Centerto_Right = 0,MaxSum_Centerto_Right = 0; 23 for(int i = center+1;i <= right;i++){ 24 Centerto_Right += a[i]; 25 if(MaxSum_Centerto_Right < Centerto_Right) 26 MaxSum_Centerto_Right = Centerto_Right; 27 } 28 return MaxSum3(MaxLeftSum,MaxRightSum,MaxSum_Centerto_Left + MaxSum_Centerto_Right); 29 } 30 int MaxSum3(int a,int b,int c) 31 { 32 return (a>b?a:b)>c?(a>b?a:b):c; 33 }
4.在线处理:时间复杂度O(n)
在线处理的规则是,从头开始求子列和,并记录当前最大子列和,若当前子列和为负,则抛弃之。代码很清楚的说明了这一规则。
个人认为在线处理的理解核心:当前子列和若为正,总有可能使之后的子列和变大的。如果当前子列和为负,则不可能是后面的子列和变大,所以抛弃。
1 //在线处理 2 int MaxSubseqSum4(int a[],int size) 3 { 4 int ThisSum=0,MaxSum=0; 5 for(int i = 0;i < size;i++){ 6 ThisSum += a[i]; 7 if(MaxSum < ThisSum) 8 MaxSum = ThisSum; 9 else if(ThisSum < 0) 10 ThisSum = 0; 11 } 12 return MaxSum; 13 }
整理自Mooc陈越 、何钦铭数据结构课程